- #1
PinguZaide
- 4
- 0
Hello everyone. Hope somebody can help.
We are given the following circuit.
http://puu.sh/70uaQ.png
We need to find the currents i1, i2 and i3 by explicitly using the mesh law.
There are no relevant equations.
So, I draw these 4 meshes on the circuit.
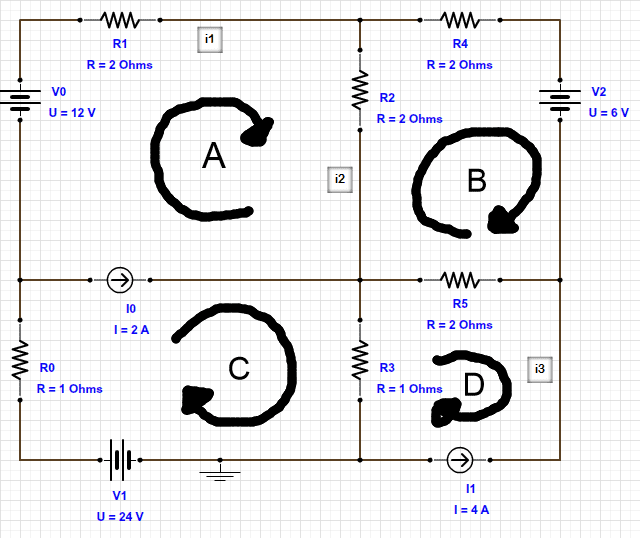
Let's call iA the current in mesh A, iB the current in mesh B, and so on.
Let's also call v_I0 the voltage at I0 and v_I1 the voltage at I1. For each current source, we assume the current enters at + and leaves at -.
Considering we already know the current in mesh D, there is no need to build an equation for that one. We only need to build the equations for meshes A, B and C.
We know that iD = 4A and that iC - iA = 2A, so that iC = 2 + iA.
I ended up with those equations.
Mesh A
12 = 2 * (iA) + 2 * (iA - iB) - v_I0
Mesh B
-6 = 2 * (iB - 4) + 2 * (iB - iA) + 2 * iB
Mesh C
24 = 1 * iC + v_I0 + 1 * (iC - 4)
After some algebra, and by substituing iC = 2 + iA, we end up with 3 equations and 3 unknowns in iA, iB and v_I0.
I end up finding iA = 6.875A, iB = 2.625A and v_I0 = 10.25V, so iC = 8.875.
Therefore, the currents that we want to know are :
i1 = iA = 6.875A
i2 = iA - iB = 4.25A
i3 = iD = 4A
The problem I have is that I used an online tool called DoCircuits to simulate the circuit, and by the result of the run, I would be suppose to have :
i1 = -4.375A, i2 = 5.25A and i3 = 4A
(Link to the circuit : http://www.docircuits.com/my-circuit/7691/2)
I therefore think there must be something I did wrong...
Thanks to anyone who helps me. :)
Homework Statement
We are given the following circuit.
http://puu.sh/70uaQ.png
We need to find the currents i1, i2 and i3 by explicitly using the mesh law.
Homework Equations
There are no relevant equations.
The Attempt at a Solution
So, I draw these 4 meshes on the circuit.
Let's call iA the current in mesh A, iB the current in mesh B, and so on.
Let's also call v_I0 the voltage at I0 and v_I1 the voltage at I1. For each current source, we assume the current enters at + and leaves at -.
Considering we already know the current in mesh D, there is no need to build an equation for that one. We only need to build the equations for meshes A, B and C.
We know that iD = 4A and that iC - iA = 2A, so that iC = 2 + iA.
I ended up with those equations.
Mesh A
12 = 2 * (iA) + 2 * (iA - iB) - v_I0
Mesh B
-6 = 2 * (iB - 4) + 2 * (iB - iA) + 2 * iB
Mesh C
24 = 1 * iC + v_I0 + 1 * (iC - 4)
After some algebra, and by substituing iC = 2 + iA, we end up with 3 equations and 3 unknowns in iA, iB and v_I0.
I end up finding iA = 6.875A, iB = 2.625A and v_I0 = 10.25V, so iC = 8.875.
Therefore, the currents that we want to know are :
i1 = iA = 6.875A
i2 = iA - iB = 4.25A
i3 = iD = 4A
The problem I have is that I used an online tool called DoCircuits to simulate the circuit, and by the result of the run, I would be suppose to have :
i1 = -4.375A, i2 = 5.25A and i3 = 4A
(Link to the circuit : http://www.docircuits.com/my-circuit/7691/2)
I therefore think there must be something I did wrong...
Thanks to anyone who helps me. :)
Last edited by a moderator: