ranju said:
So how we will proceed.. I mean.. we should just consider one coil as the reference i.e. as current in L1 is leaving the coil then the polarity of voltages of L2 & L3 will be negative at the dotted terminal..?? then with which coil reference we will decide polarity of L1..??
You don't have to decide the overall polarity of net potentials beforehand; let the math take care of sorting that out for you. It's like mesh currents, you make an assumption about directions and then do the math. Some will turn out positive and others negative, the math sorting it out.
For mutual inductors you may find it handy to insert a voltage source in series with each inductor. Orient them so that they would produce a current out the dot on their inductor. These sources are placeholders for where you'll gather together the induced voltages from the other inductors. So you'll see that the original inductors remain in the circuit and are treated as typical isolated components and the new voltage sources take on the coupling effects.
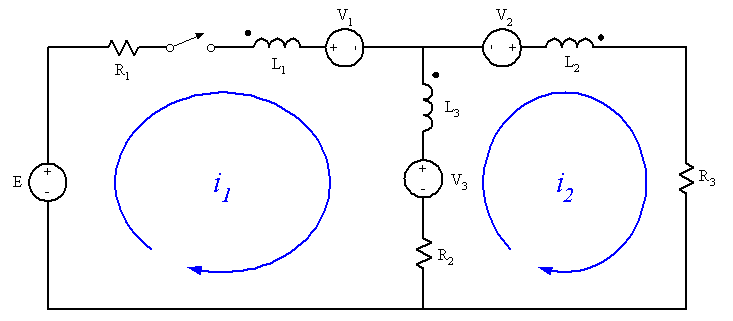
Now you can write mesh (or nodal) equations using these components easily enough. To work out the "value" of a given voltage source, look at the currents flowing through the other coupled inductors. If a current flows into a dot then add a positive term to the voltage for that inductor. If the current flows out of the dot then add a negative term. The terms are composed of the mutual inductance between the two inductors in question multiplied by the time derivative of the current in question (or if you're using the Laplace notation,##sM_{mn} I_n##, with the "s" operator implying the derivative).
For a concrete example, suppose the mutual inductances between the inductors in your circuit are ##M_{12},M_{23}, M_{13}##. For V
3 you need to consider terms due to the currents flowing through ##L_1## and ##L_2##. In the figure, ##i_1## is flowing into the dot on ##L_1## so it's contributing term will be positive: ##+s M_{13} i_1##. On the other hand, ##i_2## flows out of the dot on ##L_2##, so it contributes a negative term: ##-s M_{23} i_2##. Thus:
$$V_3 = sM_{13} i_1 - sM_{23} i_2$$
Do the same for the other sources. Take note that the current flowing through ##L_3## is ##i_1 - i_2##, so the terms contributed to ##V_1## and ##V_2## have that as their current!
