Micro Spring (DNA): Determine Energies, Find Expected Length

[GravityX]

Homework Statement

Calculate the energy of the various segments, taking into account the work done by the force F during expansion, when it expands.

Relevant Equations

none

Hi

It is about a DNA strand on which there are always two segments, the segment $A$, which is folded and has the length $l_A$ and the unfolded segment $B$, which has $l_B+\lambda$. Here is a section of the DNA

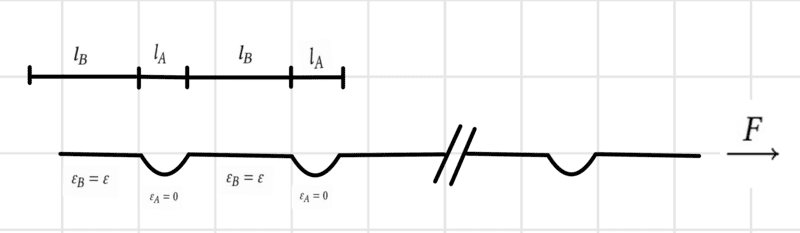
There is now, as shown in the picture, a force $F$ pulling on the strand, to unfold a segment A the energy $\epsilon$ (not dependent on the force $F$) is needed.

The first task is then:

Determine the energies of the two states of a segment
taking into account the work done by the force $F$ during expansion.

I have now thought of the following: The folded segments have the energy $\epsilon_A=0$ the force now does positive work, so the energy for these segments corresponds to $\epsilon_{AF}=F*a$.

The unfolded segments have the energy $\epsilon_B=epsilon$, now add the energy from the force $F$ so $\epsilon_{BF}=\epsilon+F*a$.

But I think that the energy is unfortunately wrong, in problem 3 you are supposed to calculate the expected length l for an unfolded segment, so $\langle l \rangle$ the result there is $\langle l \rangle=l_A+\frac{\lambda}{1+e^{\beta(\epsilon-F\lambda)}}$

Before that you had to get the partition function and the probability, I think you need this probability for the expected value.

With the partition function with $e^{-\beta \epsilon_{BF}}=e^{-\beta (\epsilon_B+Fa)}$

and the probability with $P=\frac{1}{Z}e^{-\beta (\epsilon+Fa)}$ with $Z=e^{-\beta (\epsilon+Fa)}+e^{-\beta Fa}$ is then $P=\frac{1}{e^{\beta \epsilon}+1}$

I would now have calculated the expectation value with $l*P$, so $\langle l \rangle=l_A+\lambda*P$, but unfortunately I don't get the result I'm looking for.

Is my energy simply not right or have I miscalculated somewhere?

 

[GravityX]

I looked at the question again more closely, the task says "when expanding", so the force ensures that the folded segments are unfolded, for this they must be stretched by the length $\lambda$, so the energy is thus

$$\epsilon_{AF}=F\lambda$$
$$\epsilon_{BF}=\epsilon+F\lambda$$

Would this be correct?

 

[nasu]

You are the only one who looked at the question "more closely". The rest here don't have that opportunity as you did not post the actual question.