Rampart123
- 2
- 0
- TL;DR
- Explaining the matrix elements.
Hello everyone,
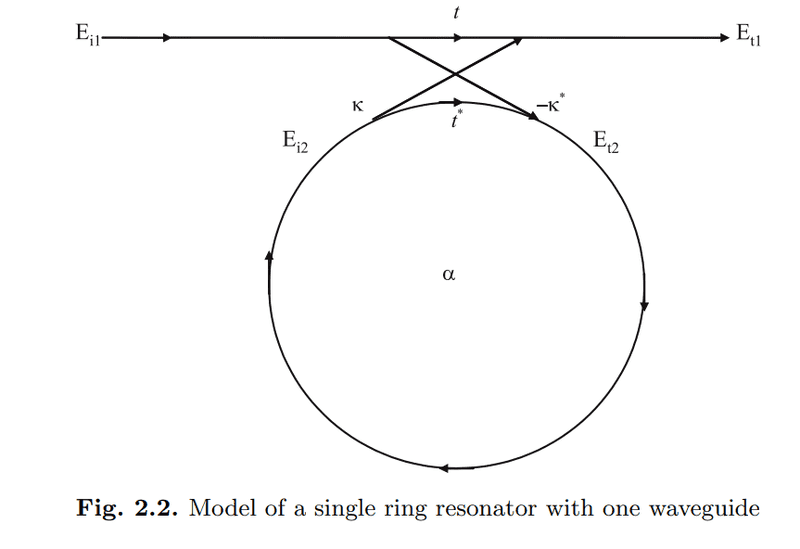
A simple ring resonator with a bus waveguide is described by:
$$ \begin{pmatrix} E_{t1}\\ E_{t2} \end{pmatrix} =
\begin{pmatrix} t & k\\ -k^* & t^* \end{pmatrix}
\begin{pmatrix} E_{i1}\\ E_{i2} \end{pmatrix} $$
I do not understand though why we have -k* and t*? Shouldn't they be also k and t?
I think the conjugation has to do with the phase of the circulating mode?
Thank you in advance!
A simple ring resonator with a bus waveguide is described by:
$$ \begin{pmatrix} E_{t1}\\ E_{t2} \end{pmatrix} =
\begin{pmatrix} t & k\\ -k^* & t^* \end{pmatrix}
\begin{pmatrix} E_{i1}\\ E_{i2} \end{pmatrix} $$
I do not understand though why we have -k* and t*? Shouldn't they be also k and t?
I think the conjugation has to do with the phase of the circulating mode?
Thank you in advance!