MarkFL
Gold Member
MHB
- 13,284
- 12
Hello MHB,
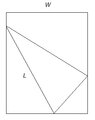
Consider a rectangular piece of paper of width $W$ laid on a flat surface. The lower left corner of the paper is bought over to the right edge of the paper, and the paper is smoothed flat creating a crease of length $L$, as in the diagram:
View attachment 1078
What is the minimal value of $L$ in terms of $W$?
Consider a rectangular piece of paper of width $W$ laid on a flat surface. The lower left corner of the paper is bought over to the right edge of the paper, and the paper is smoothed flat creating a crease of length $L$, as in the diagram:
View attachment 1078
What is the minimal value of $L$ in terms of $W$?