- #1
kieth89
- 31
- 0
Minimum distance/energy bird flight problem. (SOLVED)
SOLVED: Problem was just a simple arithmetic error (14 squared)
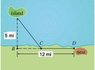
A bird is released from point A on an island 5 mi from the nearest point B on a straight shoreline. The bird flies to a point C on the shoreline and then flies along the shoreline to its nesting area D. Suppose the bird requires 10 kcal/mi of energy to fly over land and 14 kcal/mi to fly over water. The distance between point B and D is 12 miles.
View the attached diagram for an image.
If the bird instinctively chooses a path that minimizes its energy expenditure, what is its path?
Note: We are supposed to solve this using limit and derivative.
Energy used = Energy per mile * miles flown
I termed the distance from point B to C [itex]x[/itex], and the distance from point C to D [itex]12 - x[/itex].
I then found the distance from point A to point C to be [itex]\sqrt{25 + x^{2}}[/itex]. Using that I found the equation for the total energy used to be as follows:
[itex]Total Energy Used = 14\sqrt{25+x^{2}} + 10(12 - x)[/itex] This formula is the distance flown over water (Point A to C) + the distance flown over land (C to D), both of those times their energy used per mile.
I then found the derivative of that equation (zooming in (Ctrl + usually) with the browser will make the math easier to read):
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} + 10(12 - x - h) - 14\sqrt{25 + x^{2}} - 120 + 10x}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} + 120 - 10x - 10h - 14\sqrt{25 + x^{2}} - 120 + 10x}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} - 10h - 14\sqrt{25 + x^{2}}}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} - 14\sqrt{25 + x^{2}}}{h} - \lim_{h \to 0} \frac{10h}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} (\frac{14\sqrt{25+(x+h)^{2}} - 14\sqrt{25 + x^{2}}}{h}) (\frac{14\sqrt{25+(x+h)^{2}} + 14\sqrt{25 + x^{2}}}{14\sqrt{25+(x+h)^{2}} + 14\sqrt{25 + x^{2}}}) - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{186(25 + x^{2} + 2xh + h^{2}) - 186(25 + x^{2})}{14h\sqrt{25 + (x+h)^{2}} + 14h\sqrt{25 + x^{2}}} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{4650 + 186x^{2} + 372xh + 186h^{2} - 4650 - 186x^{2}}{14h(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372xh + 186h^{2}}{14h(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372x + 186h}{14(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372x + 186(0)}{14\sqrt{25 + (x+(0))^{2}} + 14\sqrt{25 + x^{2}}} - \lim_{h \to 0} 10[/itex]
Simplifying derivative:
[itex]f^{1}(x) = \frac{372x}{14\sqrt{25 + x^{2}} + 14\sqrt{25 + x^{2}}} - 10[/itex]
[itex]f^{1}(x) = \frac{372x}{28\sqrt{25 + x^{2}}} - 10[/itex]
Set derivative equal to 0 and solve:
[itex]0 = \frac{372x}{28\sqrt{25 + x^{2}}} - 10[/itex]
[itex]0 = \frac{372x - 280\sqrt{25 + x^{2}}}{28\sqrt{25 + x^{2}}}[/itex]
[itex]0 = 372x - 280\sqrt{25 + x^{2}}[/itex]
[itex]-372x = - 280\sqrt{25 + x^{2}}[/itex]
[itex]\frac{372}{280}x = \sqrt{25 + x^{2}}[/itex]
[itex]\frac{138384}{78400}x^{2} = 25 + x^{2}[/itex]
[itex]\frac{8649}{4900}x^{2} = 25 + x^{2}[/itex]
[itex]0 = 25 + x^{2} - \frac{8649}{4900}x^{2}[/itex]
[itex]0 = 25 - \frac{3749}{4900}x^{2}[/itex]
[itex]0 = (5 - \frac{\sqrt{3749}}{70}x)(5 + \frac{\sqrt{3749}}{70}x)[/itex]
[itex]0 = 5 - \frac{\sqrt{3749}}{70}x [/itex] and [itex] 0 = 5 + \frac{\sqrt{3749}}{70}x[/itex]
Since x is distance, we know it can't be negative, therefore the (5 + fraction x = 0) is not a solution, which leaves the first one.
[itex]0 = 5 - \frac{\sqrt{3749}}{70}[/itex]
[itex]-5 = -\frac{\sqrt{3749}}{70}[/itex]
[itex]-5 * - \frac{70}{\sqrt{3749}}= x[/itex]
[itex] x = 5.716238[/itex]
Which means that the distances are as follows:
The bird flies around 7.59 miles over water and around 6.28 miles over land..
However, the book says the solution for x is around 5.1 miles.
So, where did I go wrong, or did not rounding skew with my answer? The book's answer does yield around a .17 less energy use compared to mine when plugged into the original formula. But that is a very small difference. Thanks for any help.
Oh, and also, did I do my notations right with limits (ignoring LaTex putting the h to 0 beside the lim sign).
SOLVED: Problem was just a simple arithmetic error (14 squared)
Homework Statement
A bird is released from point A on an island 5 mi from the nearest point B on a straight shoreline. The bird flies to a point C on the shoreline and then flies along the shoreline to its nesting area D. Suppose the bird requires 10 kcal/mi of energy to fly over land and 14 kcal/mi to fly over water. The distance between point B and D is 12 miles.
View the attached diagram for an image.
If the bird instinctively chooses a path that minimizes its energy expenditure, what is its path?
Note: We are supposed to solve this using limit and derivative.
Homework Equations
Energy used = Energy per mile * miles flown
The Attempt at a Solution
I termed the distance from point B to C [itex]x[/itex], and the distance from point C to D [itex]12 - x[/itex].
I then found the distance from point A to point C to be [itex]\sqrt{25 + x^{2}}[/itex]. Using that I found the equation for the total energy used to be as follows:
[itex]Total Energy Used = 14\sqrt{25+x^{2}} + 10(12 - x)[/itex] This formula is the distance flown over water (Point A to C) + the distance flown over land (C to D), both of those times their energy used per mile.
I then found the derivative of that equation (zooming in (Ctrl + usually) with the browser will make the math easier to read):
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} + 10(12 - x - h) - 14\sqrt{25 + x^{2}} - 120 + 10x}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} + 120 - 10x - 10h - 14\sqrt{25 + x^{2}} - 120 + 10x}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} - 10h - 14\sqrt{25 + x^{2}}}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{14\sqrt{25+(x+h)^{2}} - 14\sqrt{25 + x^{2}}}{h} - \lim_{h \to 0} \frac{10h}{h}[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} (\frac{14\sqrt{25+(x+h)^{2}} - 14\sqrt{25 + x^{2}}}{h}) (\frac{14\sqrt{25+(x+h)^{2}} + 14\sqrt{25 + x^{2}}}{14\sqrt{25+(x+h)^{2}} + 14\sqrt{25 + x^{2}}}) - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{186(25 + x^{2} + 2xh + h^{2}) - 186(25 + x^{2})}{14h\sqrt{25 + (x+h)^{2}} + 14h\sqrt{25 + x^{2}}} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{4650 + 186x^{2} + 372xh + 186h^{2} - 4650 - 186x^{2}}{14h(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372xh + 186h^{2}}{14h(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372x + 186h}{14(\sqrt{25 + (x+h)^{2}} + \sqrt{25 + x^{2}})} - \lim_{h \to 0} 10[/itex]
[itex]f^{1}(x) = \lim_{h \to 0} \frac{372x + 186(0)}{14\sqrt{25 + (x+(0))^{2}} + 14\sqrt{25 + x^{2}}} - \lim_{h \to 0} 10[/itex]
Simplifying derivative:
[itex]f^{1}(x) = \frac{372x}{14\sqrt{25 + x^{2}} + 14\sqrt{25 + x^{2}}} - 10[/itex]
[itex]f^{1}(x) = \frac{372x}{28\sqrt{25 + x^{2}}} - 10[/itex]
Set derivative equal to 0 and solve:
[itex]0 = \frac{372x}{28\sqrt{25 + x^{2}}} - 10[/itex]
[itex]0 = \frac{372x - 280\sqrt{25 + x^{2}}}{28\sqrt{25 + x^{2}}}[/itex]
[itex]0 = 372x - 280\sqrt{25 + x^{2}}[/itex]
[itex]-372x = - 280\sqrt{25 + x^{2}}[/itex]
[itex]\frac{372}{280}x = \sqrt{25 + x^{2}}[/itex]
[itex]\frac{138384}{78400}x^{2} = 25 + x^{2}[/itex]
[itex]\frac{8649}{4900}x^{2} = 25 + x^{2}[/itex]
[itex]0 = 25 + x^{2} - \frac{8649}{4900}x^{2}[/itex]
[itex]0 = 25 - \frac{3749}{4900}x^{2}[/itex]
[itex]0 = (5 - \frac{\sqrt{3749}}{70}x)(5 + \frac{\sqrt{3749}}{70}x)[/itex]
[itex]0 = 5 - \frac{\sqrt{3749}}{70}x [/itex] and [itex] 0 = 5 + \frac{\sqrt{3749}}{70}x[/itex]
Since x is distance, we know it can't be negative, therefore the (5 + fraction x = 0) is not a solution, which leaves the first one.
[itex]0 = 5 - \frac{\sqrt{3749}}{70}[/itex]
[itex]-5 = -\frac{\sqrt{3749}}{70}[/itex]
[itex]-5 * - \frac{70}{\sqrt{3749}}= x[/itex]
[itex] x = 5.716238[/itex]
Which means that the distances are as follows:
The bird flies around 7.59 miles over water and around 6.28 miles over land..
However, the book says the solution for x is around 5.1 miles.
So, where did I go wrong, or did not rounding skew with my answer? The book's answer does yield around a .17 less energy use compared to mine when plugged into the original formula. But that is a very small difference. Thanks for any help.
Oh, and also, did I do my notations right with limits (ignoring LaTex putting the h to 0 beside the lim sign).
Attachments
Last edited: