- #1
woopydalan
- 18
- 8
- Homework Statement
- Set up the integral for both orders of integration and use the more convenient order to find the volume of the solid region bounded by the surface f(x, y) and the planes.
##f(x, y) = x##
Planes: ##z = 0##, ##y = \sqrt{25 − x^2}##, ##y = 0##
- Relevant Equations
- ##\iint\limits_R f(x,y) \, dA##
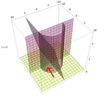
I sketched this out. With the z=0 and y=0 boundaries, we are looking at ##z \geq 0## and ##y \geq 0##
I believe ##0 \leq x \leq 5## because of the boundary of ##y=\sqrt{25-x^2}##.
This is my region
##\int_0^5 \int_0^\sqrt{25-x^2} x \, dydx ##
## =\int_0^5 xy \vert_{0}^{\sqrt{25-x^2}} \, dx##
## =\int_0^5 x\sqrt{25-x^2} \, dx##
Using U-substitution ##u = 25-x^2##, and ##du = -2x \, dx##,
## =-\frac{1}{2} \int_0^5 u^{\frac{1}{2}} \, du##
## =-\frac{1}{2} \cdot \frac{2}{3} u^{\frac{3}{2}} \vert_{0}^{5}##
##=\frac{125}{3}##
However, it seems this is not correct as when I submit this answer I get a response that it is incorrect. Am I doing something wrong with my boundaries for the integrals?
I believe ##0 \leq x \leq 5## because of the boundary of ##y=\sqrt{25-x^2}##.
This is my region
##\int_0^5 \int_0^\sqrt{25-x^2} x \, dydx ##
## =\int_0^5 xy \vert_{0}^{\sqrt{25-x^2}} \, dx##
## =\int_0^5 x\sqrt{25-x^2} \, dx##
Using U-substitution ##u = 25-x^2##, and ##du = -2x \, dx##,
## =-\frac{1}{2} \int_0^5 u^{\frac{1}{2}} \, du##
## =-\frac{1}{2} \cdot \frac{2}{3} u^{\frac{3}{2}} \vert_{0}^{5}##
##=\frac{125}{3}##
However, it seems this is not correct as when I submit this answer I get a response that it is incorrect. Am I doing something wrong with my boundaries for the integrals?
Last edited:
 ##\qquad##!
##\qquad##!