Mistake in "Foundations of Electromagnetic Theory"?

[MatinSAR]

Homework Statement

I guess there is a problem with this book in chapter 4.

Relevant Equations

Below.

The book wanna show how to find potential of a dielectric.

The problem arises when it uses a vector identity.

Still there is no problem.

My problem is that I cannot understand why $\rho_P= -div P$? I think it should be $-div' P$.
The book is wrong?

In next page it uses $-div'$

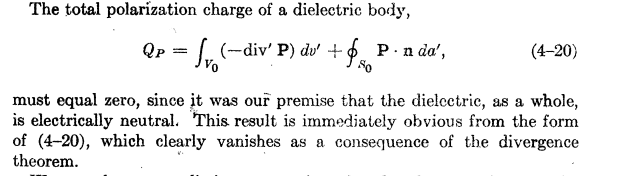
In some other pages it uses $div P$ and this confuesd me ...
My professor didn't say anything about book being wrong in this chapter and I did not take a photo of class board. So I don't have any trusted source except here ...

 

[Frabjous]

P is a function of position. Inside the integral, one is integrating in prime coordinates, so P is a function of prime coordinates. The book is correct. It‘s just notation, not physics.

 

[MatinSAR]

P is a function of position. Inside the integral, one is integrating in prime coordinates, so P is a function of prime coordinates. The book is correct. It‘s just notation, not physics.

Now I see what a poor question I've asked. Thanks @Frabjous .

 

[hutchphd]

Not a poor question. A simple and resolved question!

 

[MatinSAR]

Not a poor question. A simple and resolved question!

Thanks for your kind comment @hutchphd .

 

[hutchphd]

The question was well stated and the answer was simple. If only this was always true! Consider the time you would have needlessly wasted had you not asked the question. Confusion almost always preceeds (useful) learning.

 

[Mister T]

Confusion almost always preceeds (useful) learning.

Any time I've ever succeded in figuring something out it was always preceded by a state of confusion.