MIT OCW, 8.02, Electromagnetism: Charged Cylindrical Shell

[zenterix]

Homework Statement

I am self-studying MIT OCW's 8.02 Electromagnetism. In one of the chapters, there is the following problem (with no solution provided):

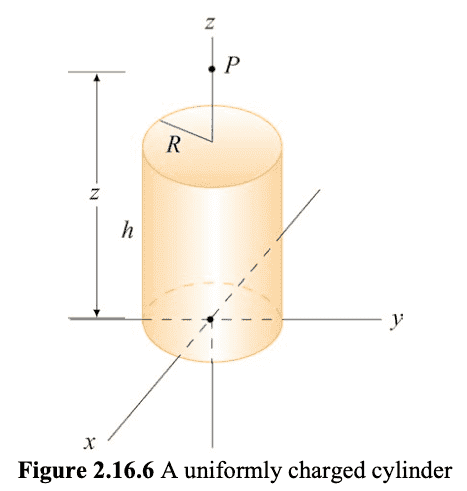
A uniformly charged circular cylindrical shell of radius $R$ and height $h$ has a total charge $Q$. What is the electric field at a point $P$ a distance $z$ from the bottoms side of the cylinder as shown in figure 2.16.6. (Hint: Treat the cylinder as a set of charged rings).

Relevant Equations

I assume that the cylinder has no bottom or top.

The charge density per area is $\rho=\frac{Q}{2\pi Rh}$.

$$dq = dl\cdot dz_{dq}\cdot \rho=\frac{Q}{2\pi h}dz_{dq}d\theta$$

where I used $dl=Rd\theta$.

The vector from $dq$ to $P$ is

$$\vec{r}=R\cos{\theta}\hat{i}+R\sin{\theta}\hat{j}+z_{dq}\hat{k}$$

and this vector has length $\sqrt{R^2+(z-z_{dq})^2}$.

Then, if $\vec{u}$ is the unit vector in the direction of $\vec{r}$, we have

$$d\vec{E}=k_e\frac{dq}{d^2}\vec{u}$$

$$=k_e\frac{Q}{2\pi h}\frac{1}{(R^2+(z-z_{dq}))^{3/2}}\vec{r} dz_{dq}d\theta$$

We want to compute

$$\int_0^{2\pi}\int_0^h d\vec{E}$$

$$=\frac{k_eQ}{2\pi h}\left [-\int_0^{2\pi}\int_0^h \frac{R\cos{\theta}}{(R^2+(z-z_{dq}))^{3/2}} dz_{dq}d\theta \hat{i} \right .$$ $$- \int_0^{2\pi}\int_0^h \frac{R\sin{\theta}}{(R^2+(z-z_{dq}))^{3/2}} dz_{dq}d\theta \hat{j}$$ $$\left . + \int_0^{2\pi}\int_0^h \frac{z-z_{dq}}{(R^2+(z-z_{dq}))^{3/2}} dz_{dq}d\theta\hat{k} \right ]$$

Here is figure 2.16.6

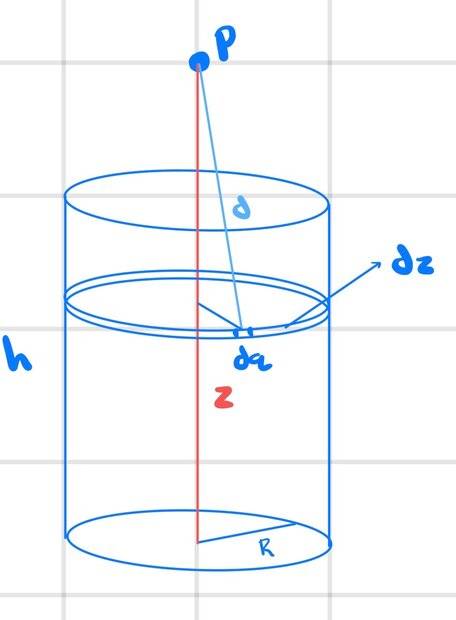
Here is the picture I drew to set up the problem

My first question is if the reasoning and integrals are correct. I used Maple to compute the three integrals. The first two result in 0, which makes sense by symmetry.

Maple can't seem to solve the last integral.

 

[kuruman]

I assume that the cylinder has no bottom or top.

You cannot assume that. The cylinder has a flat bottom in the $xy$-plane and a flat top in the plane $z=h$. Look at the picture. It's not a thin-walled tube.

Your $dq$ doesn't look right. If the cylinder has total charge $Q$, the volume charge density is $\rho=\frac{Q}{\pi R^2h}.$ Then $dq=\rho dV=\rho r'dr'~d\theta'~ dz'$ is a charge element at location $\mathbf{r}'=r'\cos\theta'~\mathbf{\hat x}+r'\sin\theta'~\mathbf{\hat y}+z'~\mathbf{\hat z}$. You need to put that in your expression for $d\mathbf{E}$ and integrate over all three primed coordinates. Yes, by symmetry only the $z$-component is non-zero. However, your integrals ignore the contributions from charge elements inside the cylinder at points $r'<R.$

 

[haruspex]

You cannot assume that. The cylinder has a flat bottom in the xy-plane and a flat top in the plane z=h. Look at the picture. It's not a thin-walled tube.

I disagree. From the shading on the 'top', what you are seeing is the inside of the cylinder.
It is described as a cylindrical shell.

 

[SammyS]

A uniformly charged circular cylindrical shell of radius $R$ and height $h$ has a total charge $Q$. What is the electric field at a point $P$ a distance $z$ from the bottoms side of the cylinder as shown in figure 2.16.6. (Hint: Treat the cylinder as a set of charged rings).$$=\frac{k_eQ}{2\pi h}\left [ \int_0^{2\pi}\int_0^h \frac{z-z_{dq}}{(R^2+(z-z_{dq}))^{3/2}} dz_{dq}d\theta\hat{k} \right ]$$

Maple can't seem to solve the last integral.

You have a typo. The $(z-z_{dq})$ in the denominator should be squared.

 

[kuruman]

I disagree. From the shading on the 'top', what you are seeing is the inside of the cylinder.
It is described as a cylindrical shell.

You are, of course, correct in disagreeing. I cannot imagine how I read "ring" and interpreted it as "disk". I guess my reading skills are deteriorating . . .

 

[zenterix]

You have a typo. The $(z-z_{dq})$ in the denominator should be squared.

Indeed, thanks.

So the integral itself is correct? It's just a question of solving it.

 

[kuruman]

Indeed, thanks.

So the integral itself is correct? It's just a question of solving it.

Yes. Except for the typo as already noted the integral is correct. Solving it should be easy with a simple substitution to get rid of the radical in the denominator.

 

[nasu]

You made it way too complicated. You don't need the integrals over angles. The field of a ring can be almost calculated in your head, it is a standard case in introductory physics. All the charge on the ring is at the same distance from the point where you calculate the field. And all the vectors contributions of the ring elements make the same angle with the vertical. The horizontal components cancel out so you only need to add the vertical components. Once you have the expresion for the field of a ring, you just need an integral over z to add all the elementary rings composing the cylindrical shell. This is why they give you that hint: use the result for the ring.