Modal frequencies of a vibrating circular membrane? (DRUM)

[mikejm]

I am in the process of trying to develop a modal drum synth. I have the following graphics as references for the frequencies of some of the first modes relative to the fundamental:

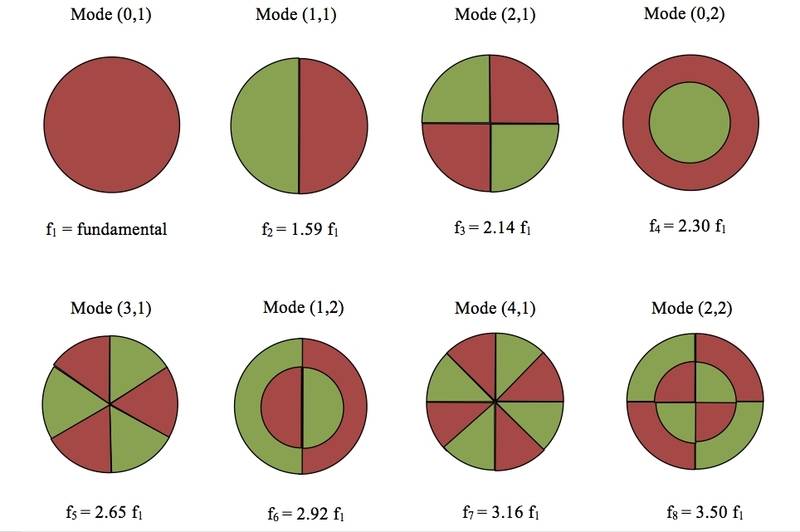
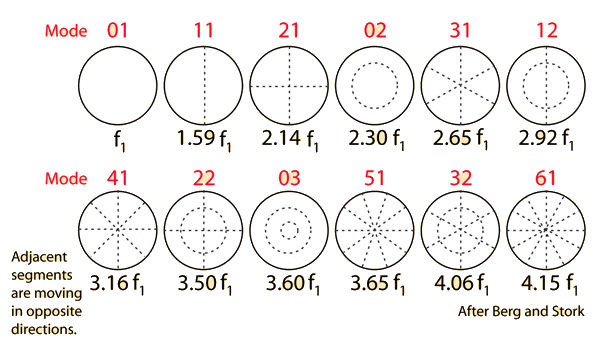
This is a good start. But I want to be able to model more modes than just that.

What is the formula required to calculate any mode as a multiplier of "f1" like above?

Eg. If I am wondering what the (7,1) mode is, how would I calculate that?

This article gets into it from what I can tell, but it's way over my head mathematically:
https://courses.physics.illinois.edu/phys406/lecture_notes/p406pom_lecture_notes/p406pom_lect4_part2.pdf

Ideally I'd like a formula I can punch (2,1) into and get 2.14 (for example).

Any help? Very appreciated if so.

Thanks,
Mike

 

[mikejm]

Here is the excerpt from that Physics 400 level course that I think summarizes the equations that are needed:

I never went past first year physics (biology & medicine guy) so I don't understand how to use these.

Any help?

If anyone has any medical questions I'm happy to answer those in return.

 

[Fred Wright]

Your issue is how to compute $x_{mn}$, which is the n-th zero of the m-th order Bessel function. There is no simple formula to do this, however there are many resources that will do the dirty work for you. A Bessel function of the first kind, $J_m\left (x\right )$, looks kind of like a periodic function but whose y values cross the x-axis at non-periodic x values. You don't need to know all about Bessel functions to solve your problem. There are online calculators that input m-n and spit back $x_{mn}$. Google "zeros of Bessel functions".
If you know how to program c++, the boost library has a function that does this as well.

 

[mikejm]

Wow. This is way harder to do than I thought it would be. Okay. Thanks.

So I've looked into what you're describing a bit, and I can find three approaches to getting it done (none of which I actually understand ). I can't code anything except HTML lol.

(If you're wondering how I'm building a drum synth without knowing how to code, it's because I'm doing it in Reaktor which doesn't require coding so much as linking modules in a logical fashion to get the signal you want.)

Anyway, here is what I've found:

1) Calculators
I found two Bessel calculators:
http://keisan.casio.com/exec/system/1180573472
http://www.mhtl.uwaterloo.ca/old/courses/me3532/js/bessel.html

The Casio one says it's for calculating zeros, but I don't know what to put in there to get what I want (or if it can give me what I want).

2) C++ with Boost
As you suggested, Fred, I found this page which seems to summarize a lot about Bessel functions and C+:
http://www.boost.org/doc/libs/1_62_0/libs/math/doc/html/math_toolkit/bessel/bessel_root.html

Is there a simple bit of code of command I could just plug into get what I want?

3) Python with MPMath
I found this seemingly simple technique using "MPMath" for Python:
http://fredrik-j.blogspot.ca/2010/07/sage-days-23-and-bessel-function-zeros.html

He gives the following example of its utility:

>>> besseljzero(1,100)
314.9434728377671624580656
​

Is that what I want? Or would it get me what I want?

Which of those would likely be the easiest way to get what I want? Thanks again. Any further help would be appreciated. I feel like a toddler.

 

[Fred Wright]

I think the easiest implementation for you is to go with the Casio calculator. In order to work that calculator enter m in the box that says "order $\nu$" and n in the box that says "ordinal number s", then press the "execute" button. Divide your answer by 2.4. Give it a go and compare with the $f_{mn}$ you already have.
Edit: The answer is by the red dot.

 

[mikejm]

Ha!

Well that is super easy. You just made my day Fred. That was a million times simpler than I was preparing for.

Thanks. Have a good one.