Modeling an earthing switch for a High Voltage Impulse Generator

[Angus Fergusson]

TL;DR

Modelling a seemingly simple mechanism that is proving to be quite challenging

Hi All,

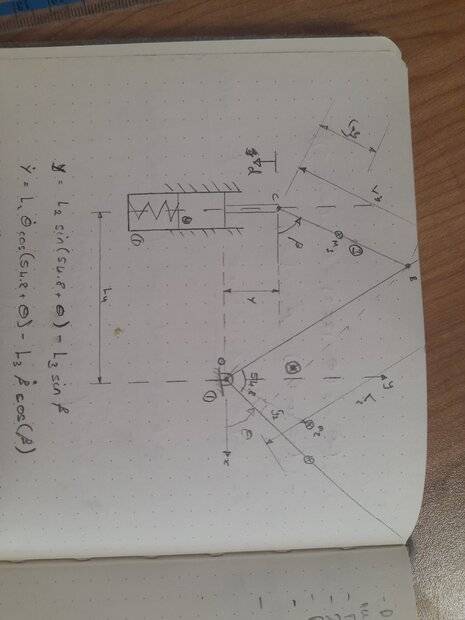
I am trying to model this mechanism for a project. It is a switch that uses a solenoid to break the contact by lifting the aluminium arm. I understand that there is most likely software out there that can do this but i would like to understand how to model this from first principals.

I have got a function for the force on the armature of the solenoid from an electromagnetic modeling software. The force on the armature is the input to the system. I want the motion of the armature, Y, as the output of the model.
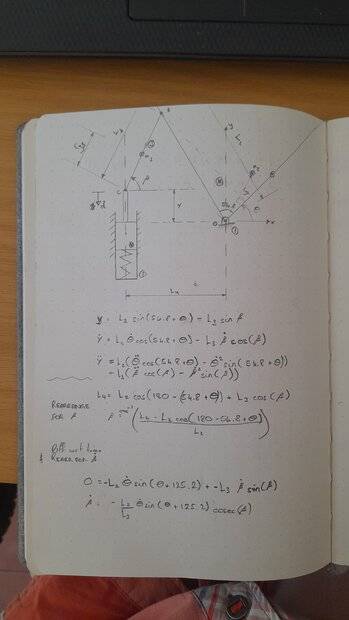
So far I have found Y and its derivatives in terms of theta and beta which are the angle of the link 2 (crank) and the angle of link 3 (con rod), respectively. I have also found beta and its derivatives in terms of theta (meaning that i effectively have Y in terms of theta). After that there is the force balance on each link. I have left friction on the armature out for now, F_mu.

At the moment I am struggling with creating the equations of motion of the armature (Ydotdot = TotalForceOnArmature/MassOfArmature). Any help would be greatly appreciated

Thanks in advance!

 

[Baluncore]

Welcome to PF.

I have got a function for the force on the armature of the solenoid from an electromagnetic modeling software. The force on the armature is the input to the system. I want the motion of the armature, Y, as the output of the model.

I assume the white arm is the earthed contact arm, and it is attached to the elbow link.
All points in the linkage appear to travel in circular arcs, except the solenoid, which moves in a straight line.

The arc through which the white arm travels, restricts the range that must be modelled.

Are you modelling the dynamic flight of the arm as a result of the predicted solenoid force, or the static force required to move the arm through, or to hold the arm in a particular position?

 

[Angus Fergusson]

Originally tried to do the dynamic flight but found the algebra for that to be far too complicated. I considered a state-space approach but do not have enough knowledge to pull that off. Ended up just doing a static force analysis to find the friction between the solenoid armature and the housing, which was then iterated to get the friction as a function of the position of the armature in the solenoid housing.

And yes you are correct with the mechanics of the linkage.

The model is no longer needed but I would love to hear if there is a better approach to the problem.