Modifying a transformation based on yaw-pitch-roll or phi-theta-psi

In summary, the conversation discusses the use of a triangular platform with markers in a 3D simulation program. The platform can translate and rotate, and there is a special marker that is always at the centroid of the platform. The goal is to constrain the orientation of this marker in a specific way using transformations, including yaw-pitch-roll and phi-theta-psi. There is some confusion about the phi-theta-psi transformation and the pictures provided are cluttered. Clarification is requested about converting between the two transformations.
  • #1
amrbekhit
11
1
[I've tried asking this question on math.stackexchange.com, but haven't got any responses, so I thought I'd try here]


I’m building a model in a 3D simulation program (MSC Adams) and part of that model is a triangular platform which can translate and rotate in the virtual world, as shown in the 2 images below:

Frame1.png


Frame2.png


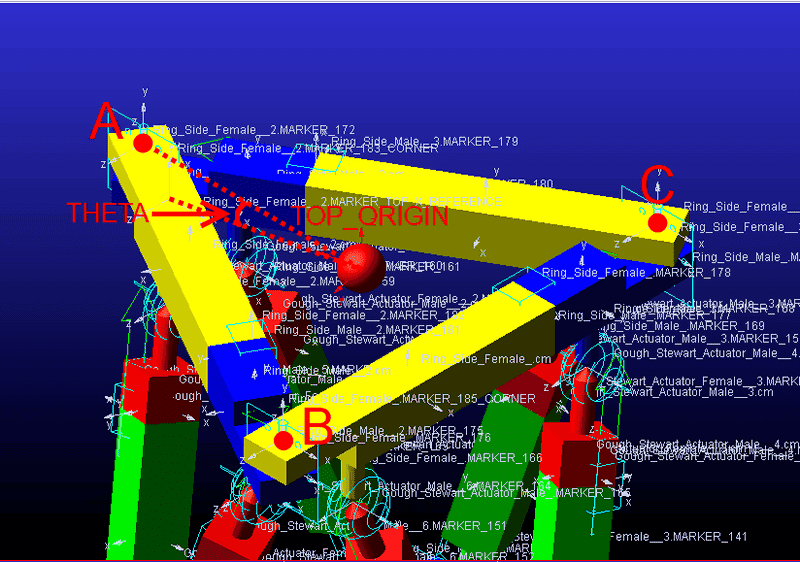
There are some markers on this platform that, when it is at its home orientation, are aligned with the global axis system (which is the orientation of markers A, B and C in the first image). These markers move and orient with the platform so that they represent the platform’s orientation with respect to the global axis system.

Now, I have a special marker (TOP_ORIGIN) that is coded so that it is always at the centroid of the corners of the triangle that form the platform (average of the coordinates A, B and C). What I’m trying to do is to also constrain the orientation of the marker as follows:

  • The X-Y plane is the same as the platform’s plane with the Z axis putting “up” away from the model.
  • The angle between the X axis and the vector XA is set to an angle, theta, which I calculate elsewhere.
  • The software gives me two ways of getting and setting the orientation of objects: yaw-pitch-roll (rotation about Z then rotation about the new Y, then rotation about the new X) and phi-theta-psi (rotation about Z then rotation about the new X, then rotation about the new Z).

How can I apply these transformations to get the marker to the orientation I want?
 
Physics news on Phys.org
  • #2
The yaw-pitch-roll transformation looks fairly standard but your description of the phi-theta-psi transformation doesn't look right. Two Z rotations is unusual, and not what I would expect from "phi-theta-psi." (P.S. I can't see what axes you are talking about because the pictures are very cluttered.)
 
  • #3
I am not sure what you are asking, amrbekhit. Do you want to convert between yaw-pitch-roll and phi-theta-psi? Can you clarify your question?
 

1. What is the difference between yaw-pitch-roll and phi-theta-psi transformations?

The main difference between these two transformations is the order in which the rotations are applied. In a yaw-pitch-roll transformation, the rotations are applied in the order of yaw (rotation around the z-axis), pitch (rotation around the y-axis), and roll (rotation around the x-axis). In a phi-theta-psi transformation, the rotations are applied in the order of phi (rotation around the x-axis), theta (rotation around the y-axis), and psi (rotation around the z-axis).

2. How do I modify a transformation based on yaw-pitch-roll or phi-theta-psi?

To modify a transformation based on yaw-pitch-roll or phi-theta-psi, you will need to use a rotation matrix or quaternion. These mathematical representations can be used to perform the necessary rotations in the correct order to achieve the desired transformation.

3. Can I use yaw-pitch-roll or phi-theta-psi to rotate an object in 3D space?

Yes, both yaw-pitch-roll and phi-theta-psi transformations can be used to rotate an object in 3D space. These transformations are commonly used in computer graphics and robotics to orient objects in a specific direction.

4. Are yaw-pitch-roll and phi-theta-psi interchangeable?

No, yaw-pitch-roll and phi-theta-psi are not interchangeable. The order in which the rotations are applied can greatly affect the resulting transformation. It is important to use the correct transformation for the desired outcome.

5. Can I combine yaw-pitch-roll and phi-theta-psi transformations?

Yes, it is possible to combine these transformations, but it is important to use the correct order of rotations. For example, if you want to combine a yaw-pitch-roll transformation with a phi-theta-psi transformation, the yaw-pitch-roll rotation should be applied first, followed by the phi-theta-psi rotation.

Similar threads

B Rotating a point in 3-space through an angle about some vector
    • Linear and Abstract Algebra
Replies
2
Views
1K
A Euler vs. Tait (steady precession vs... what?)
    • Classical Physics
Replies
1
Views
797
Rotation matrix of three intrinsic rotations
    • Mechanical Engineering
Replies
3
Views
471
Yaw,Pitch and Roll Multiplication
    • Linear and Abstract Algebra
Replies
4
Views
3K
MCNP6.2 - Combination of transformations
    • Nuclear Engineering
Replies
1
Views
1K
Applying 3 Concurrent Angular Velocities to Vectors
    • Linear and Abstract Algebra
Replies
1
Views
2K
I "Map" point between coordinate systems
    • Linear and Abstract Algebra
Replies
5
Views
2K
A Corresponding case of steady precession but for Tait-Bryan angles
    • Classical Physics
Replies
1
Views
547
Combine two pitch, yaw, roll rotations
    • Linear and Abstract Algebra
Replies
6
Views
9K
Extracting yaw, pitch, roll from transformation matrix
    • Linear and Abstract Algebra
Replies
5
Views
12K

Hot Threads

Recent Insights

Back
Top