"Map" point between coordinate systems

[RichardWattUK]

TL;DR Summary

Mapping 3D Cartesian points between coordinate systems

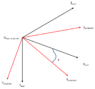
I've taken on a new job recently where I'm having to maintain an existing application that generates a points profile to drive a CNC machine and part of it projects points from an axial plane (which represents the machine's working axis) onto another plane which (I think) acts as as a global/world coordinate system - I'm guessing as I'm still finding the documentation from the people who worked on it a few years ago and have since left.

The application uses Newton's method to find an angle of rotation to map a point on the profile in the axial plane across to the projected plane, which works in the majority of cases, but there are some where it doesn't due to being unable to find the appropriate angle of rotation to use within 30 iterations and with an accuracy of +- 0.0001.

I've been looking at matrix-based rotations and transformations to do this, including something based on the original code that was used to do this translation which worked in a different way by finding the distance along the Y axis for the new point using Newton's method with an accuracy of +- 0.00001 in a maximum of 30 iterations.

But I can't get anything to work - I've been looking at working with the radius and angle to the point on the axial plane (the Y coordinate is taken as = 0 so we're only looking at X and Z coordinates) to the origin, but not getting anywhere with that.

I've attached an image showing how the planes & their axes are related, with "γ" on the diagram representing the projection angle between the axial and projected planes.

So my question is related to whether anyone knows of a way to perform this mapping/projection please? It's been about 20 years since I last looked at these kinds of calculations so I'm a bit out of practice with them.

 

[fresh_42]

Do you have three non planar points with original and target coordinates?
You talked about accuracy but not about which numbers do you really have to perform transformations on.

 

[RichardWattUK]

Unfortunately, no to the 3 non planar points - the routine that performs the mapping was written to convert one point at a time and is called from within a loop to work through the profile.

The accuracy is the limit placed on the Newton iteration method loops for accepting the root value.

Each point is represented with a width (X coordinate, $X_a$), a radius (Z coordinate, $Z_a$) and an outward normal angle ($\theta_a$).

I have made some progress using the cosine of the projection angle on the X & Z coordinates to work out the projected X & Z coordinates - I'm typing this at home but my notes are back in the office, so I'll update again when I've got them - basically using:

$$X_p = cos \gamma \cdot X_a$$
$$Y_p = cos \gamma \cdot Z_a$$

When the existing method works, the projected point is offset from the axial point by a small amount on both the X and Z axes, a small amount being in the order of 0.01 mm.

I'm currently looking at how to calculate the new outward normal angle ($\theta_p$).

 

[Stephen Tashi]

I've attached an image showing how the planes & their axes are related, with "γ" on the diagram representing the projection angle between the axial and projected planes.

The diagram doesn't explain what you mean by "the radius".

 

[RichardWattUK]

The diagram doesn't explain what you mean by "the radius".

My apologies - I should have labelled the X axis is "the width" and the Z axis is "the radius".

 

[Stephen Tashi]

My apologies - I should have labelled the X axis is "the width" and the Z axis is "the radius".

That doesn't explain the situation. You haven't explained what type of coordinate systems are being used. Are both coodrindate systems cartesian coordinate system? If so, how is the relationship between them defined? What parameters define the relationship? For two general cartesian coordinate systems, a single parameter $\gamma$ would be insufficient.