- #1
Sara583
- 4
- 0
Homework Statement
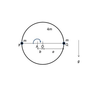
Two particles, each of mass m, are attached one to each end of a diameter PQ of a uniform circular disk, of mass 4m, radius a with its centre at O. The system is free to rotate about a horizontal axis through A, a point on PQ such that OA = b as indicated in the diagram below. The system is released from rest when PQ is horizontal.[/B]
Determine the Moment of Inertia of the system about the axis A, in terms of integer constants, a , b and m.
Determine the angular velocity of the disk plus masses when PQ is vertical. Enter your answer in terms of integer constants, a, b and the acceleration due to gravity g.
Homework Equations
I=ma^2
parallel axis equation I=Icentre of mass + md^2
The Attempt at a Solution
I already calculated the moment of inertia using the parallel axis theorem, which gave me 4ma^2+6mb^2, but now I'm not entirely sure how to relate the acceleration to the moment of inertia to find the angular velocity. Any suggestions very welcome.
Thanks