SUMMARY
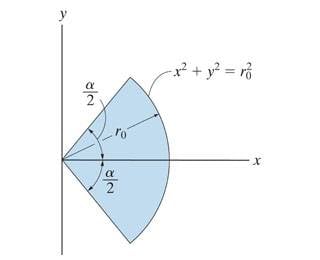
The discussion focuses on calculating the moment of inertia of a shaded area about the x-axis using the equation I(x) = y²dA. The participants explore the integration process, highlighting the challenges of handling complex integrals and the importance of careful algebraic manipulation. A specific integral involving arcsin and arctan identities is discussed, revealing that a small error, such as a misplaced parenthesis, can lead to significant discrepancies in results. Ultimately, the correct approach involves detailed verification of each step in the integration process to avoid mistakes.
PREREQUISITES
- Understanding of moment of inertia concepts
- Familiarity with double integrals and their applications
- Knowledge of trigonometric identities, particularly arcsin and arctan
- Proficiency in algebraic manipulation and simplification techniques
NEXT STEPS
- Study the derivation of the moment of inertia for various shapes
- Learn advanced integration techniques, including integration by parts and substitution
- Explore the use of computational tools like Wolfram Alpha for integral verification
- Practice solving complex integrals involving trigonometric functions and their identities
USEFUL FOR
Students and professionals in engineering, physics, and mathematics who are involved in mechanics and structural analysis, particularly those focusing on calculating moments of inertia and mastering integration techniques.