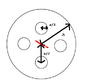
Calculating Moment of Inertia for a Cylinder with Varying Radii?

[TBoy]

Please, help me to solve this problem.

I need to calculate moment of inertia, I, for this body on picture:
- mass o the body is m
- radius of the big cylinder is a
- radius of the small cylinders is a/3


Thanks for your help!

 

[stingray78]

Well you have that I=Integral(r^2*dm)
Then u have the density=Mass/Volume (I'm supposing it's a cylinder)
then dm=density*dV
Then you solve I=Integral(r^2*density*dx*dy*dz) where r^2=x^2+y^2.
now you have the full cylinder without the holes.
Do the same for the holes and sum (with a minus of course)

Good luck

 

[stingray78]

Ohh if you're having trouble with the holes just integrate but using r as a vector. So you do r=x+(cos(tethta), sen(theta)) where x is the vector from the oringin to the center of the wholes. Using that r just repeat it for the 4 circles (it's simetrical). Just remember that when integrating area in polar coordiantes dA=dx*dy=r*dr*dTheta

Cheers

 

[stingray78]

Ohh and one more thing! remember that in vectors r^2=inner product (r,r)
:)
If u get stressed check tubepolis.com for some funny videos jeje. Look for triger happy those r really fun.

 

[TBoy]

Thanks, will try it later when i will have some time! It seams logical! :)