Moment of Inertia - equilateral triangle

[zwingtip]

Homework Statement

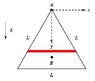
[PLAIN]http://img59.imageshack.us/img59/9484/fp5.gif
to find the moment of inertia through point A

Homework Equations

I = \int{r^2dm}

The Attempt at a Solution

Used a double integral from point A:

<br /> \displaystyle\int_{0}^{h}\displaystyle\int_{-L/2}^{L/2}\rho(x^2+y^2)dxdy<br /> = \rho\displaystyle\int_{0}^{h}\(\frac{1}{12}L^3+Ly^2)dy = \rho(\frac{1}{12}L^3h+\frac{1}{3}Lh^3)<br />

with
h=\frac{\sqrt{3}}{2}L
and
\rho=\frac{M}{\frac{1}{2}Lh}

and ended up with I = \frac{2}{3}ML^2

This seems too simple to be right. Help?

 

[ehild]

It is not correct. The integration with respect to x has to go from the left side of the triangle to the right side.


ehild

 

[zwingtip]

Okay, in that case, I have no idea how to integrate it. Help? I tried integrating it as a function of y and got

\frac{3\sqrt{3}}{16}ML^2

But that doesn't seem right either.

 

[ehild]

<br /> <br /> \displaystyle\int_{0}^{h}\displaystyle\int_{-y/\sqrt 3}^{y/\sqrt 3}\rho(x^2+y^2)dxdy<br /> <br />

ehild

 

[zwingtip]

Thanks. I'll try it.

 

[zwingtip]

Is the answer

\frac{5}{12}ML^2
?

 

[Delzac]

Hi,

Can anyone explain how x^2 + y^2 was obtained. I understand how to do double integral, but i am not adapt at applying it.

Delzac

 

[zwingtip]

In the moment of inertia, x^2+y^2 is r^2 (pythagorean theorem)

 

[ehild]

Is the answer

\frac{5}{12}ML^2
?

I got the same result.

ehild