Moment of Inertia of a 4 rod system

[Aurelius120]

Homework Statement

Calculate the Moment of Inertia of each and determine the greatest:

Relevant Equations

MOI=mr2

This was the question

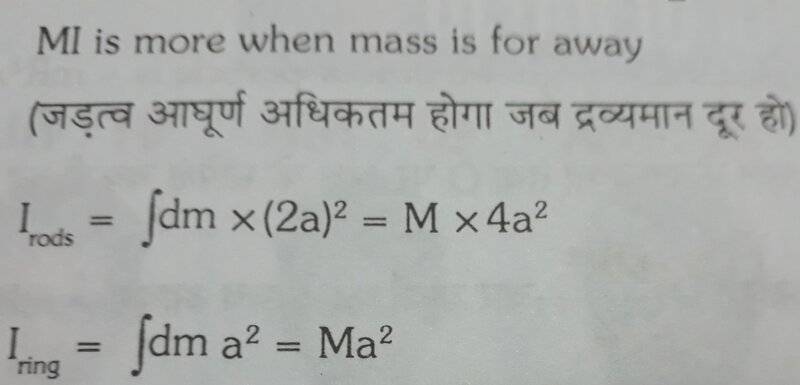
(The line below is probably some translation of upper line in different language)

For disc it was ma^2/2
For ring it was ma^2
For square lamina it was 2ma^2/3
For rods
It was different

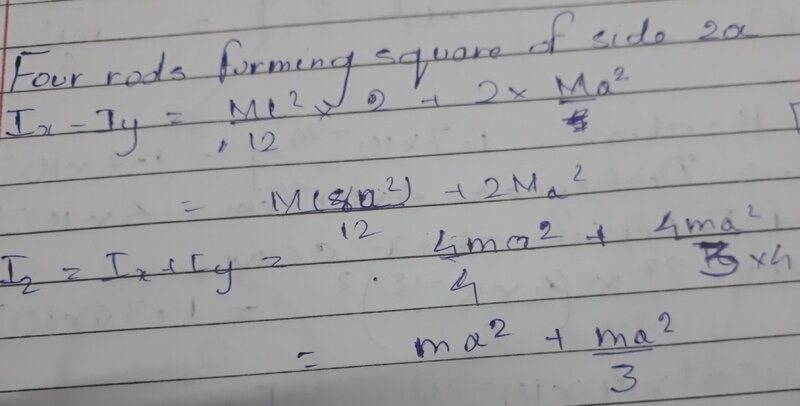
Please explain

Thank You

 

[TSny]

I don't know what was being calculated by this equation

The hand-written calculation is a little messy and hard to follow, but it looks correct for the 4 rods making a square.

 

[Aurelius120]

It probably calculated the MOI of the system (because it was the solution given in the booklet)

Also my MOI came out to be
(m/4)×(8a^2)÷12 + 2×(m/4)×a^2
[About x and y axes]

&&

(ma^2)+(ma^2)/3

{About z axis}

 

[TSny]

Also my MOI came out to be
(m/4)×(8a^2)÷12 + 2×(m/4)×a^2
[About x and y axes]

Ok, you are saying that $I_{\rm x\, axis} = I_{\rm y\, axis} = \frac{m}{4} \frac{8a^2}{12} + 2 \frac{m}{4}a^2$
That looks correct.
It would be nice to simplify the result.

&&

(ma^2)+(ma^2)/3

{About z axis}

Here you are using $I_{\rm z\,axis} = I_{\rm x\,axis}+I_{\rm y\,axis} = 2I_{\rm x\,axis} = ma^2 + \frac{ma^2}{3}$.
This looks correct. Of course you can simplify this result to just one term.