Moment of inertia of a non-homogenous cylinder

[Karol]

Homework Statement

What is the moment of inertia round the axis of a cylinder length L, mass M and a linear distribution of mass with the radius R, zero at the center.

Homework Equations

Moment of inertia: ##I=mr^2#3

The Attempt at a Solution

The density ρ=kr. what is k? the total mass is M
$$M=\int_v dz\;dr\;(r\;d\theta)\cdot kr=k\int_0^L dz \int_0^{2\pi}d\theta \left( \frac{1}{3}r^3 \right)_0^R\;\rightarrow k=\frac{3M}{2\pi R^3L}$$
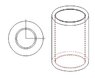
To calculate I for the cylinder i take concentric rings of infinitesimal thickness dr (drawing) and with the full height L of the cylinder:
$$dm=2\pi rL\cdot dr\cdot kr,\; dI=dm\cdot r^2=2\pi kL\cdot r^4 dr$$
$$I=2\pi kL\int_0^R r^4dr=\frac{1}{5}2\pi k L R^5$$

 

[Orodruin]

Did you have a question? Your attempt looks reasonable. You can insert your expression for k in the final expression and some factors will cancel.

 

[Karol]

Thanks, i just wanted to know if it's true