Moment of Inertia of Rod About Axis XX': ML2/3sin2α

[Aditya1998]

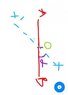
1. The problem statementα, all variables and given/known data

The moment of inertia of a Rod over an
Axis XX' passing through the center of mass of the Rod at an angle α is-

Homework Equations

Moment of Inertia of Rod about the end, I =ML²/3

The Attempt at a Solution

I=ML²/3
Answer of the question is ML²/3sin²α

I didn't understood how sin² came because even if we shift OL over the axis XX' then

OX=OLcosα

[/B]

 

[Doc Al]

Hint: Set up an integral.

 

[haruspex]

I didn't understood how sin2 came because even if we shift OL over the axis XX' then
OX=OLcosα

The distance along the axis, OX, does not affect moments about the axis. The distance of interest is from the XX' axis to the points on the rod.