Idividebyzero
- 64
- 0
1.
2. I = (x/x) M L ^ 2
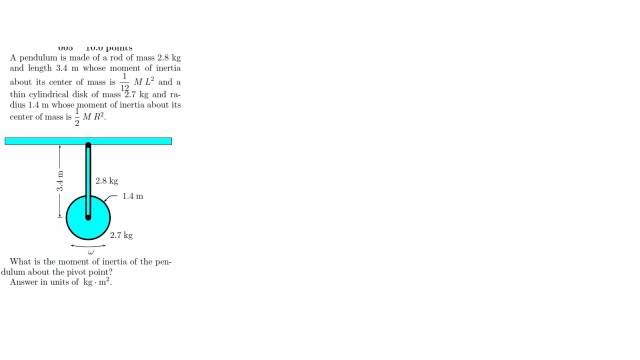
3i honestly have no idea where to go with this. i do have an attempt so please don't laugh. I took the (L) for the moment for the rod = 3.4 m and divided it into 2 parts. R sub 1 and R sub 2. With R sub 2 on half of R sub 1. The equation i got using the R sub 1 i have the moment for the disc: I = mdiscr12 + Icm and for the R sub 2 i have the moment for the rod: Ir= mrrrod2 + Icm from here i don't know what to do with them or if I am even correct in my assumptions
2. I = (x/x) M L ^ 2
3i honestly have no idea where to go with this. i do have an attempt so please don't laugh. I took the (L) for the moment for the rod = 3.4 m and divided it into 2 parts. R sub 1 and R sub 2. With R sub 2 on half of R sub 1. The equation i got using the R sub 1 i have the moment for the disc: I = mdiscr12 + Icm and for the R sub 2 i have the moment for the rod: Ir= mrrrod2 + Icm from here i don't know what to do with them or if I am even correct in my assumptions