Silken
- 4
- 0
Hi everyone
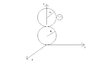
I want to find out the moment of intertia tensor of the graphic below.
parallel axis theorem
We know the moment of inertia for one sphere, that's given, so I don't have to calculate it explicit.Now I have trouble understanding the moment of inertia tensor. It looks like the following:
I=\begin{pmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix}
I understand that Ixx, Iyy and Izz are the moments of inertia regarding to x y and z but I don't understand what Ixy Ixz Iyz etc. 'means'. I just can't picture it. Furthermore I tried to find the xx yy and zz, I found out :
I_{xx}=I_{yy}=\frac {54} {5} MR^{2}+9r^{2}m
and
I_{zz}=\frac 4 5 MR^{2}+(R+r)^{2}M
But how do I find the xy xz etc. I know I just have to calculate thre more, because the tensor is symmetrical. But I don't know how do to it. Is my solution right thus far?
Thanks for your help
Homework Statement
I want to find out the moment of intertia tensor of the graphic below.
Homework Equations
parallel axis theorem
The Attempt at a Solution
We know the moment of inertia for one sphere, that's given, so I don't have to calculate it explicit.Now I have trouble understanding the moment of inertia tensor. It looks like the following:
I=\begin{pmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{pmatrix}
I understand that Ixx, Iyy and Izz are the moments of inertia regarding to x y and z but I don't understand what Ixy Ixz Iyz etc. 'means'. I just can't picture it. Furthermore I tried to find the xx yy and zz, I found out :
I_{xx}=I_{yy}=\frac {54} {5} MR^{2}+9r^{2}m
and
I_{zz}=\frac 4 5 MR^{2}+(R+r)^{2}M
But how do I find the xy xz etc. I know I just have to calculate thre more, because the tensor is symmetrical. But I don't know how do to it. Is my solution right thus far?
Thanks for your help