Frod
- 1
- 0
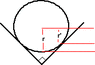
Hello, I have been given a loop-the-loop problem to do. Now the problem I have isn't with conservation of mechanical or rotational energy, it's with the moment of inertia of the solid sphere. Usually it would be (2/5)*M*r^2 however the sphere is rolling on a "V" track (see image). I get the correct answer if I leave the moment of inertia as (2/5)*M*r^2, however, shouldn't it be different as it is no longer rolling on r, instead it is rolling on r' (see image)?
I have worked out that the angular velocity will be [(2)^0.5*v]/r, where r is the radius of the sphere and v the velocity of the sphere. Any help would be greatly appreciated. Thank you.
Frod.
I have worked out that the angular velocity will be [(2)^0.5*v]/r, where r is the radius of the sphere and v the velocity of the sphere. Any help would be greatly appreciated. Thank you.
Frod.