Conservation of Momentum in Collision of Balls: Solving for Unknowns

[unscientific]

Homework Statement

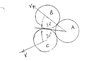
The problem is given in the picture: (please refer to the 2 pictures below, thank you!)

I'm having trouble with the last part...

Homework Equations

Conservation of momentum in both x and y - directions.

The Attempt at a Solution

From symmetry it can be seen that ball D would be directly below ball C, with ball C moving at speed of (2/5)sqrt(3)*u at an angle of 30 degrees below horizontal.

Here's my attempt using the x-y direction conservation of momentum

Taking downwards and leftwards as positive,

Horizontally:
There would be no transfer in horizontal momentum to ball D, hence ball C still would have a horizontal velocity of: (3/5)u

Vertically (downwards as positive):
sqrt(3)/5 * u = v_c cosθ + v_D

Energy equation:
(12/25)u² = (v_c)² + (v_D)²


That leaves me with 2 equations with 3 unknowns, v_c, v_D and θ.


I tried using a new approach, but would like to ask if this obeys the laws of physics:

Horizontal speed of c: unchanged = (3/5)u

Considering collision "vertically":
can i simply do the momentum equation by solely considering only the vertical velocities?

(1/5)sqrt(3)* u = V_c,y + V_D

Again only considering energy in the vertical direction: ( i know this is wrong as energy is not a vector!):

(9/25)u² = (v_c,y)² + (v_D )²


This allows me to solve the problem, but is this the right approach?

Here's a quick, not-so-rigorous proof: vx² + vy² = v'², multiplying (1/2)m throughout... gives us the split energy equation!)

 

[gneill]

...can i simply do the momentum equation by solely considering only the vertical velocities?

Yes. Momentum is conserved separately and collectively for the components of the motion.

 

[BruceW]

It is wrong to consider energy in the vertical direction. So far, you've got 2 equations, and 3 unknowns (as you said):

Energy equation:
(12/25)u2 = (vc)2 + (vD)2

Vertically (downwards as positive):
sqrt(3)/5 * u = vc cosθ + vD

And there is one more equation: the horizontal momentum. This will involve u, vc and theta. So once you write that out, you have 3 equations and 3 unknowns, which you can then solve.

 

[BruceW]

The reason that you get the correct answer by considering only the components of KE from the y direction is because the speeds of the objects in the x direction happen to be the same before and after collision. So in this case, you could consider the vertical components of KE, but this only works by coincidence. In most problems, doing this will get you a nonsense answer.

 

[unscientific]

It is wrong to consider energy in the vertical direction. So far, you've got 2 equations, and 3 unknowns (as you said):

Energy equation:
(12/25)u2 = (vc)2 + (vD)2

Vertically (downwards as positive):
sqrt(3)/5 * u = vc cosθ + vD

And there is one more equation: the horizontal momentum. This will involve u, vc and theta. So once you write that out, you have 3 equations and 3 unknowns, which you can then solve.

I tried to consider the horizontal momentum, but that simply gives me:

(3/5)u = (3/5)u

since ball D only moves downwards and has 0 horizontal momentum.

 

[BruceW]

Well, you've written that the final vertical speed of ball c is vc cos(theta) So what will the horizontal speed of ball c be?