Momentum conservation at vertex in Feynman Diagrams

[Dixanadu]

Hey guys,

I need help with conserving momentum at these vertices (this is Bhabha scattering):

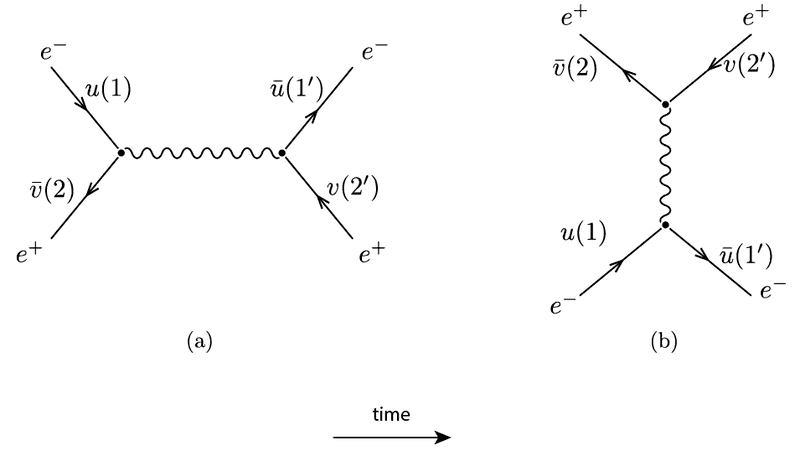
So in Diagram (a), the first vertext to the left. The incoming momenta are p_{1}+p_{2}. The outgoing momentum I'll call it p. So...shouldnt I have p_{1}+p_{2}=p? Furthermore, is the propagator correct if I write it like this:

\dfrac{-i\eta_{\mu\nu}}{(p_{1}+p_{2})^{2}+i\epsilon}?

Now I don't know how to conserve momentum at the second vertex, neither do I know how to do it for any vertex in Diagram (b). It's really confusing...

 

[Orodruin]

You do momentum conservation for each vertex separately. First define in which direction your momentum is flowing (for external lines and s-channel propagators there is a natural choice, for t-channel just pick one direction) and then put momentum in equal to momentum out and then you are done. As you have noticed, this will let you get rid of some momenta, such as the s-channel propagator momentum. You might also want to rewrite things in terms of Mandelstam variables, but that is another issue.

 

[Dixanadu]

I still don't get it though. For example I have a photon propagator in each case (not sure if that's T channel or S channel) so does that have a fixed direction of momentum?

I'm still confused...I kind of see what to do but I just don't know how. Could you help me do a couple of vertices just so I get the hang of it? (also please tell me if I got the one right in my first post)

 

[mfb]

so does that have a fixed direction of momentum?

What do you mean with "direction of momentum"? The direction used in your calculation is arbitrary, but following the time axis in s-channel (like you did) is useful. A direction in space does not matter here.

 

[Dixanadu]

Hmm. I guess it would help if you told me whether I'm right in my first post about the momentum conservation...

 

[mfb]

Yes that is right.

 

[ChrisVer]

Momentum is conserved, means that if you inititally had P= p_1 + p_2 momentum, then at the end you are having p_3 + p_4 = P momenta.
So p_1 + p_2 = p_3 + p_4.

When you calculate cross sections (or amplitudes) things become much clearer by having the delta function in your integrals: \delta^{(4)} (p_1 + p_2 - p_3 - p_4 )

If you want to insert somehow the momentum carried by the propagator q then this delta can give you the conservation of momenta in each vertex:
\delta^{(4)} (p_1 + p_2 -q) (or p_1+p_2 =q) and \delta^{(4)} (q - p_3 - p_4 ) (or q=p_3+p_4).

As for the t-channel, you can do the same...apply a conservation of momentum delta function to each vertex, eg \delta^{(4)} (p_1 + q - p_3) for your upper vertex. Everything is done so that you will eventually get that the initial sum of momentum= final sum of momentum, encoded in the delta function you integrate over:
\delta^{(4)} (p_1 + p_2 - p_3 - p_4 )
which corresponds to the 1+2 \rightarrow 3+4