- #1
FlatEarth
- 6
- 0
I was doing a physics problem on my homework and was not sure which of the three questions below i got wrong as I got a 2/3. I believe the second one might be wrong, but I'm not to sure.
Two fan carts labeled A and B are placed on opposite sides of a table with their fans pointed in the same direction as shown in the figure below. Cart A is weighted with iron bars so it is twice as heavy as cart B. When the fans are turned on, they cause the air to exert a constant force on the cart independent of its mass. Assume that friction is small enough to be neglected. The fans are set with a timer so that after they are switched on, they stay on for a fixed length of time, Δt, and then are turned off.
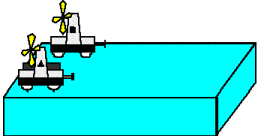
A. Just after the fans are turned off, which of the following statements are true about the momenta of the two carts? pA = pB
B. Just after the fans are turned off, which of the following statements are true about the kinetic energies of the two carts? KEA
C. Which of the following statements are true? The momentum of each cart is conserved.
Answer 1:
pA = pB
Answer 2:KEA < KEB
Answer 3:The momentum of each cart is conserved.
Two fan carts labeled A and B are placed on opposite sides of a table with their fans pointed in the same direction as shown in the figure below. Cart A is weighted with iron bars so it is twice as heavy as cart B. When the fans are turned on, they cause the air to exert a constant force on the cart independent of its mass. Assume that friction is small enough to be neglected. The fans are set with a timer so that after they are switched on, they stay on for a fixed length of time, Δt, and then are turned off.
A. Just after the fans are turned off, which of the following statements are true about the momenta of the two carts? pA = pB
B. Just after the fans are turned off, which of the following statements are true about the kinetic energies of the two carts? KEA
C. Which of the following statements are true? The momentum of each cart is conserved.
Answer 1:
pA = pB
Answer 2:KEA < KEB
Answer 3:The momentum of each cart is conserved.