dahoom102
- 12
- 2
- Homework Statement
- Two particles P and Q of masses 3 kg and 2 kg respectively are moving along the same straight line on a smooth horizontal surface. The particles collide. After the collision both the particles are moving in the same direction, the speed of P is 1 m/s and the speed of Q is 1.5 m/s. The magnitude of the impulse of P on Q is 9N s. Find:
a) Speed and direction of P before the collision
b) Speed and direction of Q before the collision
- Relevant Equations
- I=m(v-u)
Pf=Pi
Hi
I've tried solving this question but it seems that I flipped the direction of the impulse, what did I interpret wrong? the question didn't give any clue on their direction before so I couldn't infer the direction of the impulse. It also just gave me the magnitude without the direction. I would appreciate if you could help me know why is my diagram wrong.
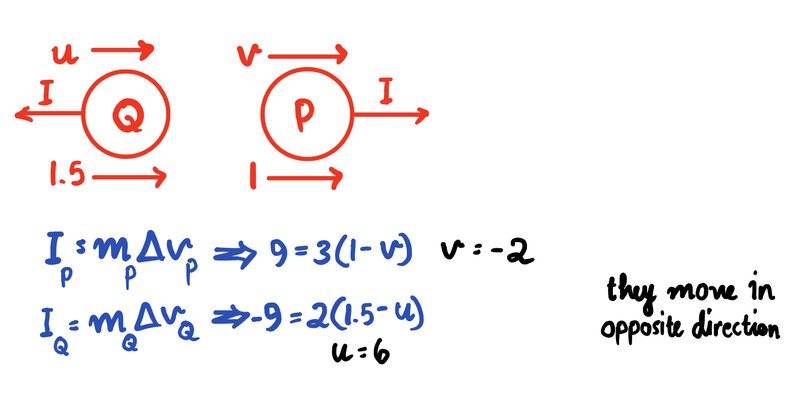

I've tried solving this question but it seems that I flipped the direction of the impulse, what did I interpret wrong? the question didn't give any clue on their direction before so I couldn't infer the direction of the impulse. It also just gave me the magnitude without the direction. I would appreciate if you could help me know why is my diagram wrong.