oskarbjo
- 3
- 0
< Mentor Note -- thread moved to HH from the technical physics forums, so no HH Template is shown >[/color]
Hi!
I am having a bit trouble understanding how to determine the wavelength bandwidth for a monochromator. If anyone could suggest what to look for it'd be really nice. The problem is formulated something like this:
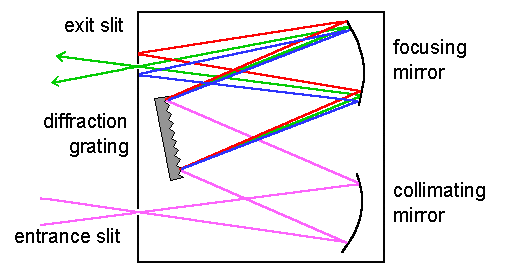
White light is aimed into a monochromator. The monochromator consists of a grating (with slit spacing d) that the light is reflected from. This light is then aimed to a slit with width t. How will the interval of wavelengths that comes out from the slit depend on t and d?
I don't see how this information is enough to determine the bandwidth. If anyone could give me a hint I'd be really thankful.
Edit: I missed there was a forum for homework. Requested thread to be moved
Oskar
Hi!
I am having a bit trouble understanding how to determine the wavelength bandwidth for a monochromator. If anyone could suggest what to look for it'd be really nice. The problem is formulated something like this:
White light is aimed into a monochromator. The monochromator consists of a grating (with slit spacing d) that the light is reflected from. This light is then aimed to a slit with width t. How will the interval of wavelengths that comes out from the slit depend on t and d?
I don't see how this information is enough to determine the bandwidth. If anyone could give me a hint I'd be really thankful.
Edit: I missed there was a forum for homework. Requested thread to be moved
Oskar
Last edited by a moderator: