Motion of charge at centre of ring

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

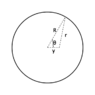
I started by calculating potential energy at a distance x(<<R). I used the approximation and differentiated the result to get an expression for force which came out to be
$$F=-\frac{kQqx}{2R^3}\Rightarrow a=-\frac{kQqx}{2mR^3}$$

This is an easily recognisable expression. The charge performs SHM about the center of ring. Hence the time it takes to return back is $\pi/ \omega$ where $\omega=\sqrt{\frac{kQq}{2mR^3}}$ but I get the wrong answer from this. I think my approach is wrong as I haven't used the mass of the ring.

Any help is appreciated. Thanks!

 

[haruspex]

It's not clear whether the ring is free to move, but since the mass i given, suppose that it is.
You could take the common mass centre as the frame of reference. This will move at constant velocity, but you don't need to worry about that.

 

[Saitama]

It's not clear whether the ring is free to move, but since the mass i given, suppose that it is.
You could take the common mass centre as the frame of reference. This will move at constant velocity, but you don't need to worry about that.

I am still unsure what to do. If the charge displaces x from its original position, the ring also displaces x in the opposite direction. But what can I do with this? Should I find potential energy again at this instant?

 

[haruspex]

I am still unsure what to do. If the charge displaces x from its original position, the ring also displaces x in the opposite direction.

It won't also be x, since the masses are different. The ratio is known. The force varies according to the total distance. This should give you a simple factor adjustment to what you had previously. (Do you know what the answer should be?)

 

[Saitama]

It won't also be x, since the masses are different. The ratio is known.

Yes I realized it but I couldn't edit my post due to some reason.

The force varies according to the total distance. This should give you a simple factor adjustment to what you had previously. (Do you know what the answer should be?)

No I don't know the answer.

Do I have to multiply it (the force expression) by a factor of 9/4?

 

[haruspex]

Do I have to multiply it (the force expression) by a factor of 9/4?

For a given displacement of the central mass, the distance will be 3/2 times as great as in your original calculation, no? So the force should be less?

 

[Saitama]

For a given displacement of the central mass, the distance will be 3/2 times as great as in your original calculation, no? So the force should be less?

It's my fault. I should have written down all the steps on how I arrived at the expression for force.

The distance of the charge from the center of ring is 3x/2. Let 3x/2=y. Consider an element of length $Rd\theta$ on the ring. Charge on this part is $\lambda(Rd\theta)$. $r$ can be calculated using law of cosines i.e
$$r=\sqrt{R^2+y^2-2Ry\cos\theta}=R\sqrt{1+\frac{y^2}{R^2}-\frac{2y}{R}\cos\theta}$$

The potential at distance y from centre due to this small particle on ring is
$$dV=\frac{k\lambda Rd\theta}{r}$$
Substituting r in the above expression, using the approximation and integrating the expression from 0 to $2\pi$, I get
$$V=\frac{kQ}{4R}\left(\frac{y^2}{R^2}+4\right)$$
Potential energy is $qV$. Substituting y=3x/2 and differentiating the expression w.r.t x, I get the same expression of force as before but multiplied by 9/4.

Looks correct?

 

[haruspex]

I get the same expression of force as before but multiplied by 9/4.

Sorry, you're right. Does that give the right answer now?

 

[Saitama]

Sorry, you're right. Does that give the right answer now?

I will have to give it a try, I was just double checking my work.

So the time it takes to return back is $\pi/\omega$?

EDIT: Unfortunately, that's incorrect. :(

 

[consciousness]

I will have to give it a try, I was just double checking my work.

So the time it takes to return back is $\pi/\omega$?

EDIT: Unfortunately, that's incorrect. :(

I think that the effect of the motion of the ring is not limited to the force. Since the position of the particle is w.r.t. to the ring we have to find the time period of the rings motion also ( which I think will be an SHM). After this we must find the LCM of their time periods.

 

[haruspex]

I think that the effect of the motion of the ring is not limited to the force. Since the position of the particle is w.r.t. to the ring we have to find the time period of the rings motion also ( which I think will be an SHM). After this we must find the LCM of their time periods.

The two cannot have different periods. The common mass centre must move with constant velocity. If x is the displacement of the particle from the common centre then the movement of the ring should merely magnify the movement of the particle in relation to the ring.
However, I now think there's something wrong with multiplying the force by 9/4. My gut feel says it should only be 3/2. According to the original calculation, the restorative force increases linearly with displacement from centre of ring (hence SHM). With the ring's movement taken into account, the displacement from centre of ring is 3/2 times the particle's displacement from the common centre, x, so the force should be 3/2 times as great. But what is the flaw in the revised calculation from first principles? It would have to be in the differentiation step, namely, that the differentiation should be wrt y, not x. I just can't quite convince myself.

Edit: If the same analysis were done from the ring's perspective, displacement from common centre being x', the displacement relationship would now be y = 3x'. But the force must be the same. Therefore F = kQqy/(2R³), not kQqx/(2R³).

 

[Saitama]

The two cannot have different periods. The common mass centre must move with constant velocity. If x is the displacement of the particle from the common centre then the movement of the ring should merely magnify the movement of the particle in relation to the ring.
However, I now think there's something wrong with multiplying the force by 9/4. My gut feel says it should only be 3/2. According to the original calculation, the restorative force increases linearly with displacement from centre of ring (hence SHM). With the ring's movement taken into account, the displacement from centre of ring is 3/2 times the particle's displacement from the common centre, x, so the force should be 3/2 times as great. But what is the flaw in the revised calculation from first principles? It would have to be in the differentiation step, namely, that the differentiation should be wrt y, not x. I just can't quite convince myself.

Edit: If the same analysis were done from the ring's perspective, displacement from common centre being x', the displacement relationship would now be y = 3x'. But the force must be the same. Therefore F = kQqy/(2R³), not kQqx/(2R³).

I tried multiplying the force by 3/2. It gives the correct answer.

Yes, I think you are right, the differentiation should be w.r.t x. Thank you for the help!

 

[TSny]

Using a general theorem about reducing a two-body system to an effective one-body system, you can consider the ring as fixed as long as you use the "reduced mass" of the system for the mass of the point charge. In this problem the reduced mass is 2 g (or 2/3 of the mass of the point charge). I think this has the same effect as not using the reduced mass but multiplying the force by 3/2.