What is the tension in a charged ring?

[etotheipi]

Homework Statement

The ring I'll assume to have negligible thickness, and linear charge density $\lambda$, as well as a radius $R$.

Relevant Equations

N/A

I tried considering a little piece of the ring (shaded black below) subtending angle $d\theta$, and attempted to find the electric field in the vicinity of that piece by a summation of contributions from the rest of the ring:

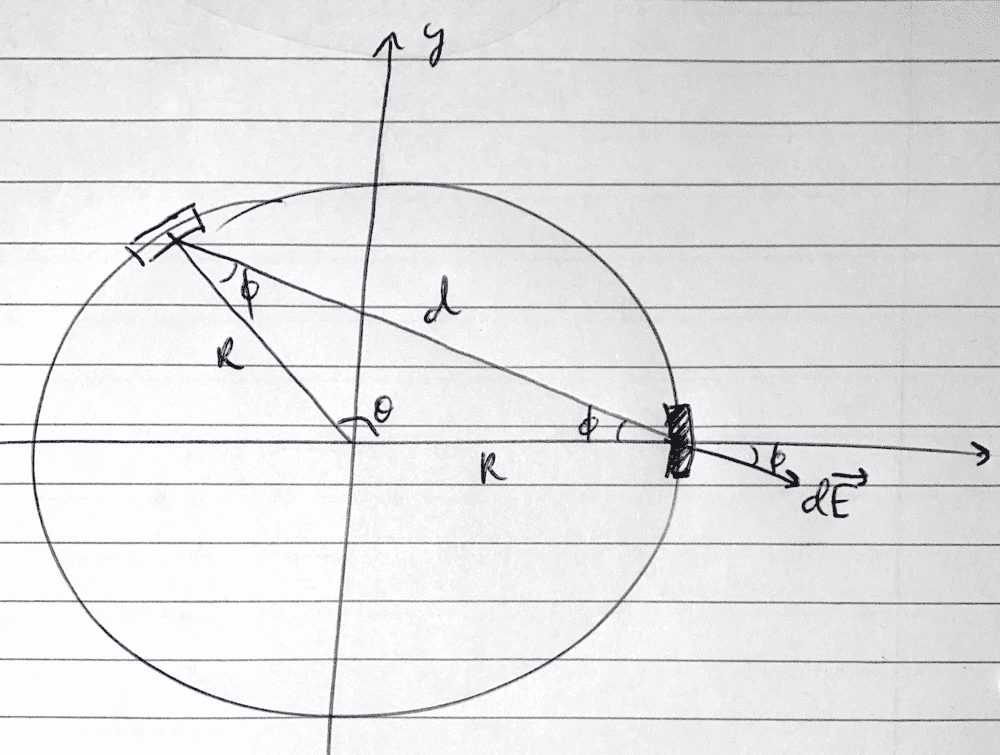
$$dE_x = \frac{dq}{4\pi \epsilon_0 d^2} \cos{\phi} = \frac{\lambda R d\theta}{4\pi \epsilon_0 \cdot 2R^2(1-\cos{\theta})}\cos{\phi}$$ $$E_x = \int_0^{2\pi} \frac{\lambda \sin{\frac{\theta}{2}}}{8\pi \epsilon_0 R(1-\cos{\theta})} d\theta = \frac{\lambda}{8\pi \epsilon_0 R} \int_0^{2\pi} \frac{\sin{\frac{\theta}{2}}}{1-\cos{\theta}} d\theta $$ Problem is, that thing diverges because the denominator goes to zero at the boundaries (the indefinite is easy enough to solve by changing $1-\cos{\theta} = 2\sin^2{\frac{\theta}{2}}$). If we call $$I = \int_{0}^{2\pi} \frac{\sin{\frac{\theta}{2}}}{1-\cos{\theta}} d\theta$$ then the electrostatic force on the piece in terms of this is $$F_e = (\lambda R d\theta) \frac{\lambda I}{8\pi \epsilon_0 R} = 2T\sin{\frac{d\theta}{2}} \approx T d\theta$$ and the tension would be, under the usual equilibrium constraint, $$T = \frac{\lambda^2 I}{8\pi \epsilon_0} = \frac{q^2 I}{32 \pi^3 R^2 \epsilon_0}$$but that doesn't make much sense if $I$ is infinite. I wondered if anyone could help out? Perhaps it is the case that the electric field diverges at the ring, but in that case, how could I modify my calculations to get a sensible answer? Because I am fairly sure that in reality the tension will not be infinite . Thanks!

 

[PeroK]

Can you explain why the assumed physical scenario may not be valid?

Hint: consider a finite set of charges.

 

[etotheipi]

Can you explain why the assumed physical scenario may not be valid?

Hint: consider a finite set of charges.

I'm not too sure. If you replace the homogenous linear charge with a bunch of individual point charges spaced at regular intervals, then the charge density $\rho$ will diverge at the point charges (since we can make the domain $V$ arbitrarily small), and be zero elsewhere. That will mean that $\vec{E}$ is undefined at the point charges.

It would seem that the electric field diverges here too, in the radial direction, at the ring.

 

[PeroK]

I'm not too sure. If you replace the homogenous linear charge with a bunch of individual point charges spaced at regular intervals, then the charge density $\rho$ will diverge at the point charges (since we can make the domain $V$ arbitrarily small), and be zero elsewhere. That will mean that $\vec{E}$ is undefined at the point charges.

It would seem that the electric field diverges here too, in the radial direction, at the ring.

Yes, you have two problems. Trying to calculate the field on a line charge and trying to calculate a tension on a perfect circle.

 

[etotheipi]

Yes, you have two problems. Trying to calculate the field on a line charge and trying to calculate a tension on a perfect circle.

I'm happy with the first part, in some cases like a 3D shell of charge we can get perfectly well defined electric fields at the boundary, but not so much for a line of charge, and evidently this example too.

But I wonder what is wrong with calculating tension on a perfect circle? A similar technique is used to look at mechanical capstans, or in 3D we could consider a small surface element of a soap bubble and derive an equilibrium equation to relate surface tension to the pressure differential.

 

[PeroK]

I'm happy with the first part, in some cases like a 3D shell of charge we can get perfectly well defined electric fields at the boundary, but not so much for a line of charge, and evidently this example too.

But I wonder what is wrong with calculating tension on a perfect circle? A similar technique is used to look at mechanical capstans, or in 3D we could consider a small surface element of a soap bubble and derive an equilibrium equation to relate surface tension to the pressure differential.

Perhaps you could get the two infinities to cancel out? What if you consider a small element on the right, and calculate the tension on that and take the limit as the size of the element goes to zero?

I don't know if that would work out. It's just an idea.

 

[etotheipi]

Perhaps you could get the two infinities to cancel out? What if you consider a small element on the right, and calculate the tension on that and take the limit as the size of the element goes to zero?

I don't know if that would work out. It's just an idea.

Actually that's a pretty good idea, have some (no longer infinitesimal) control region on the right that subtends an angle $\alpha$ or something, and try to come up for an expression for the electrostatic force on that.

It's slightly more complicated maths-wise and I'm not so sure how best to do it yet, but I think that would give something useful! Let me think about it for a while

Thanks!

 

[Adesh]

I'm happy with the first part, in some cases like a 3D shell of charge we can get perfectly well defined electric fields at the boundary, but not so much for a line of charge, and evidently this example too.

But I wonder what is wrong with calculating tension on a perfect circle? A similar technique is used to look at mechanical capstans, or in 3D we could consider a small surface element of a soap bubble and derive an equilibrium equation to relate surface tension to the pressure differential.

We cannot a get a good form for electric field at points of the circle beacuse the field is not radial. I doubt if there exist a nice mathematical form of electric field other than on the central axis.

Our (I mean yours) loop has to have some outward stretching for tension to exist by that external force, otherwise all the tension is due to the material of loop being bent to form a circle.

 

[haruspex]

Line charges are not physically valid. They only work as approximations of the field due to a wire at distances from the wire rather greater than its thickness. At the wire itself you get an infinite field.

You might be able to resolve it by considering the field at a point on the line as due to separate sections: a nearby region, treated as a straight hollow cylinder, and the rest treated as a zero thickness circular arc.
Figuring out where to do the cutover will be interesting.

Edit: no, can't assume it is ok to treat it as a straight cylinder.. the field would have no component in the direction of interest. Need some way to bound the component.

 

[etotheipi]

Line charges are not physically valid. They only work as approximations of the field due to a wire at distances from the wire rather greater than its thickness. At the wire itself you get an infinite field.

You might be able to resolve it by considering the field at a point on the line as due to separate sections: a nearby region, treated as a straight hollow cylinder, and the rest treated as a zero thickness circular arc.
Figuring out where to do the cutover will be interesting.

Thanks, I didn't know that was a general property.

Your suggestion is quite interesting, it seems like a very good idea. Like you mentioned, I am not sure how to judge where to split it up. I'll try and play around with it for a bit tomorrow morning!

I was also thinking, if the line charges are not physical, then might it be easier to model the loop with a torus of non-zero cross sectional area, probably as an insulator with uniform charge density to keep things simple? Maybe this will also be too complicated. Perhaps it is also possible to calculate the potential energy of such an arrangement, and from that derive some sort of electric force. I don't know; in any case, puzzles for tomorrow .

 

[Vanadium 50]

Why do you want to use calculus?

 

[etotheipi]

Why do you want to use calculus?

No particular reason, but it's the only way in I could see. Is there a better way?

For a 3D shell you can use superposition ideas because it's easy to find the electric field inside and outside, but here it doesn't seem as straightforward.

 

[Vanadium 50]

Yes...not calculus.

Can you replace the field from a ring of charge with that from a point? Can you determine the energy of a ring of charge using that? How does it depend on Δr? If the ring were also a spring, what would the change in its energy be as a function of Δr?

 

[etotheipi]

Yes...not calculus.

Can you replace the field from a ring of charge with that from a point? Can you determine the energy of a ring of charge using that? How does it depend on Δr? If the ring were also a spring, what would the change in its energy be as a function of Δr?

Interesting! Right now I probably can't because I am about to fall asleep, but a few things that come to mind before then...

It's not immediately obvious to me how to find the effective point charge, but I'm guessing it's going to be in the centre of the ring. I would have thought you obtain the self energy by then integrating up the energy density $\frac{1}{2}\epsilon_0 E^2$ over all space, but you said no calculus, so that can't be right...

I am not sure; a point charge would have a field strength that falls of as an inverse square with radius but the one I derived initially was only inversely proportional to the first power of $R$. Finding the point charge seems to be the key bit, though I'm a little stuck

In 3D you can find an outward pressure by differentiating w.r.t. volume, but here we can't do that. Maybe taking the derivative w.r.t. $r$ gets something with dimensions of force, but I don't know how to interpret this exactly?

Maybe you could replace the linear charge with $n$ point charges equally distributed, then the potential energy would be a summation involving $^n C_2$ terms each of which is a bit like $$\frac{q^2}{4 \pi \epsilon_0 \sqrt{2R^2(1-\cos{\frac{2\pi m}{n}})}}$$ perhaps $\frac{dU}{dr}$ is useful.

Maybe it will be more obvious in the morning

 

[Vanadium 50]

Google shell theorem.

 

[Delta2]

I was also thinking, if the line charges are not physical, then might it be easier to model the loop with a torus of non-zero cross sectional area, probably as an insulator with uniform charge density to keep things simple? Maybe this will also be too complicated.

That's what I was thinking from the first moment I saw this thread. Math will get complex but I think its the only nice way I see to get rid of the infinity of the electric field. Probably the end result will be something that has afunction of $(R_{in}-R_{out})$ in the denominator ($R_{in},R_{out}$ the inner and the outer radius of the torus), and it will also diverge if $R_{in}=R_{out}$ which is the case that the torus degenerates to a circle.

 

[haruspex]

it will also diverge if $R_{in}=R_{out}$ which is the case that the torus degenerates to a circle.

Not necessarily. There are two limit processes here, that involved in the integration and that in letting the radius of the wire tend to zero. Swapping the order so that the integration is done first might not lead to the same result.

 

[Adesh]

One thing that is coming to my mind constantly is if we have a steel wire (negligible thickness) then we know that it can stretched and tension can be developed in it by straining it. Now, imagine we charge the steel wire with continuous charge distribution, as all the charges are same they will repel each other and therefore we might be tempted to say there would exist a tension in the steel wire due to electric repulsion but when we go to mathematics for the calculation of repulsive force we find that charges are so close to each other that there will be an infinite repulsion on any segment of the wire.

So, how about first calculating the tension on a straight wire and then moving on to the circular loop.

 

[Delta2]

We ll run into similar problem trying to calculate the tension in a straight wire of infinitesimal thickness. The reason is that by Gauss's law in differential form we ll have that $$\nabla\cdot\mathbf{E}=\frac{\rho}{\epsilon_0}$$ and because the wire is of infinitesimal thickness the charge density $\rho$ will be a dirac delta function $$\rho(\mathbf{r})=\lambda\delta(\mathbf{r}-\mathbf{r_0}),\mathbf{r_0}\in L$$, hence $$\nabla\cdot\mathbf{E(r_0)}=\infty$$.

I believe that infinite divergence of the E-field in this case means that the E-field becomes infinite. In some other cases it means that the E-field does a jump between two finite values.

 

[Delta2]

Not necessarily. There are two limit processes here, that involved in the integration and that in letting the radius of the wire tend to zero. Swapping the order so that the integration is done first might not lead to the same result.

I don't agree, I think even if we do the integration first, we ll get something that will give infinities as $R_{in}\to R_{out}$

 

[Adesh]

Well we can think about this problem in an analogous way as drop of water. The pressure inside the drop is more and the pressure outside is less, so water drop should expand but it’s the surface tension that is preventing it from increasing its radius.

For the present case, we need to have a total force on the loop, which we can find by finding the electric force on a element and integrating all over the loop, then this total outward force will be equal to tension in the equilibrium case.

 

[etotheipi]

Google shell theorem.

I can prove the shell theorem for a shell, but not a ring. I think this problem is actually very easy in 3D, since the inside field is zero and field just outside the surface is $\frac{\sigma}{\epsilon_0}$. By the principle of superposition we immediately know that the field at the surface from the rest of the shell is finite and equal to $\frac{\sigma}{2\epsilon_0}$, from which we can get an internal electrostatic pressure (for instance, it is just the energy density ). Then we could finally consider a surface element acted upon by 4 tension forces and solve for equilibrium.

But I don't know of any shell theorem in the 2D case? I wonder if there is a generalisation we can make?

That's what I was thinking from the first moment I saw this thread. Math will get complex but I think its the only nice way I see to get rid of the infinity of the electric field. Probably the end result will be something that has afunction of $(R_{in}-R_{out})$ in the denominator ($R_{in},R_{out}$ the inner and the outer radius of the torus), and it will also diverge if $R_{in}=R_{out}$ which is the case that the torus degenerates to a circle.

I think I might try this. At the moment I'm not too sure how to go about finding any electric fields, but it's surely possible?

 

[Adesh]

We cannot get an explicit expression for the force at any point on the boundary of the loop, therefore we shall not be able to calculate the tension.

 

[haruspex]

I don't agree, I think even if we do the integration first, we ll get something that will give infinities as $R_{in}\to R_{out}$

Quite possibly, just saying you should not assume that.

 

[Vanadium 50]

But I don't know of any shell theorem in the 2D case

Did you look at the proof? (Hint: I already know the answer to that)

Normally I don't like providing complete (or near complete) solutions, but people keep pushing you into taking integrals.

Define r₁=R and r₂ = R+ΔR.
The ring is a spring of spring constant k, so the energy in it is 1/2 kx². The difference in energies as it goes from r₁=R to r₂ is Aπ²kRΔR, so the tension is Aπ²kR. A is completely calculable, but I leave calculating it as an exercise to the student.

The total charge is 2πRλ, Because of the shell theorem, I can treat this as coming from a single point at the center of the loop. The energy at point r₁ is [1/4πε₀]( 2πRλ )²/r₁ (do you see why? Particularly why 2πRλ is squared?), and at r₁ is [1/4πε₀]( 2πRλ )²/r₂. The difference between this is BΔR.

B is completely calculable, but I leave calculating it as an exercise to the student.

Consideration of energy means Aπ²kRΔR = BΔR, which let's you solve for k in terms of A and B. You plug that back into T = Aπ²kR.

You don't need to calculate electric fields, and you certainly don't need to be taking integrals hither and yon. You do need to understand the symmetries of the problem, and you have to understand the ideas behind the various rules and formulas, and not just memorize the outcome.

Finally, a few hours calculating can save you from a few minutes thinking.

 

[haruspex]

Because of the shell theorem, I can treat this as coming from a single point at the center of the loop.

THis is the part that seems to puzzle everyone else on the thread. As far as I know, that is only for spherical symmetry, which we do not have here.

 

[Vanadium 50]

That's why I said "look at the proof".
The 3-D shell theorem is proved by summing up rings.

 

[etotheipi]

Define r₁=R and r₂ = R+ΔR.
The ring is a spring of spring constant k, so the energy in it is 1/2 kx². The difference in energies as it goes from r₁=R to r₂ is Aπ²kRΔR, so the tension is Aπ²kR. A is completely calculable, but I leave calculating it as an exercise to the student.

The total charge is 2πRλ, Because of the shell theorem, I can treat this as coming from a single point at the center of the loop. The energy at point r₁ is [1/4πε₀]( 2πRλ )²/r₁ (do you see why? Particularly why 2πRλ is squared?), and at r₁ is [1/4πε₀]( 2πRλ )²/r₂. The difference between this is BΔR.

B is completely calculable, but I leave calculating it as an exercise to the student.

Consideration of energy means Aπ²kRΔR = BΔR, which let's you solve for k in terms of A and B. You plug that back into T = Aπ²kR.

There are a few things here which I do not follow. Okay so our ring is a spring, if it's natural length is zero (?) then the increment in energy when undergoing an increment of $\Delta R$ is $$\Delta E = \frac{4\pi^2 k}{2}(R^2 + 2R\Delta R + \Delta R^2 - R^2) \approx 4\pi^2 k R \Delta R$$ Then you identify tension as $4 \pi^2 k R$. This is the first bit I don't understand. Sure, the work done by the force of tension is the negated increment of the elastic potential energy, however here the tension forces do not act in the radial direction, so obtaining the force from this work doesn't seem as straightforward as division by $\Delta R$.

Next you say we can treat the charge as being in the centre of the ring; But here there is no sufficient spherical symmetry for the shell theorem to apply (in fact, this would only work if the electric force obeyed an inverse first power law).

But even then, I can't tell what you are computing the energy of. The equation $\frac{(2\pi R \lambda)^2}{4\pi \epsilon_0 r}$ would be the electric potential energy of a point charge of charge $2\pi R \lambda$ and a ring of charge density $\lambda$ at a radius $R$ around the point charge, or indeed alternatively two such point charges. But then I thought you replaced the ring with a single point charge, so where does the other body in the pair come from?

I might miss your point but currently it seems there are too many missing pieces.

 

[haruspex]

That's why I said "look at the proof".
The 3-D shell theorem is proved by summing up rings.

Sure, but isn't the point at which the field is being considered on the axis of the ring in that proof? Here it is on the perimeter.

 

[Vanadium 50]

If you don't want to follow the proof, here's the heuristic. In the plane of the ring, field lines are radial by symmetry. I can always replace the ring by one a factor of 2 (or 10, or a million) smaller without changing the field strength anywhere it wasn't zero. (Obviously points that were inside and are now outside see different fields). Do that as many times as you want and you get your ring arbitrarily close to a point.