Force of one distribution of charge on another

[archaic]

Homework Statement

I need help on solving this exercise :
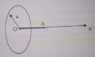
We have a ring of radius = $a$ uniformly charged (total charge = $Q$) and on its axis a segment $OA$ (length = $a$ also) of uniformly distributed positive electric charges with the charge density $\lambda'$ and of total charge = $Q$ (the same as the ring).

I'm asked to determine the total force $\vec{F}$ that the ring's distribution is exerting on the segment's distribution.

Homework Equations

$\vec{F}=q.\vec{E}$

The Attempt at a Solution

First of all we have, for a point $M$ of $OA$ :
$\vec{F}_{Ring/M}=k\frac{Q.\lambda'dz}{a^2+z^2}\vec{u_z}$ with $k\frac{Q}{a^2+z^2}\vec{u_z}=$ the electric field created at $M$.
$\Rightarrow \vec{F}_{Ring/OA} = kQ\lambda'\int_0^a \frac{dz}{a^2+z^2}\vec{u_z} = kQ\lambda'\frac{\pi}{4a}\vec{u_z}$
Where have I gone wrong?
Thank you!

 

[wrobel]

I believe that the result must have the following shape
$$\mathrm{Const}\cdot\int_0^\pi \int_0^a\frac{zdzd\varphi}{(z^2+a^2)^{3/2}}$$
where $\varphi$ is the angle on the circle

 

[haruspex]

Where have I gone wrong?

You need just the component of the field in the z direction.

 

[archaic]

You need just the component of the field in the z direction.

So multiply by a cosine? But shouldn't that be already taken into account since we're given the charge of the ring? I mean we're supposing that each point of the ring is creating a force.

 

[haruspex]

So multiply by a cosine? But shouldn't that be already taken into account since we're given the charge of the ring? I mean we're supposing that each point of the ring is creating a force.

But what direction is the force from a small element of the ring? Is it along the z axis?

 

[archaic]

But what direction is the force from a small element of the ring? Is it along the z axis?

Yes, considering symmetries

 

[haruspex]

Yes, considering symmetries

No, that's the overall result. What are the magnitude and direction of the force from a small element of the ring? What component of that is along the z axis?

 

[archaic]

No, that's the overall result. What are the magnitude and direction of the force from a small element of the ring? What component of that is along the z axis?

That would be $\vec{F}=k\frac{dq_{ring}.dq_M}{a^2+z^2}cos\theta .\vec{u_z}$

 

[archaic]

Well the force of the whole ring on a point M would be $$\vec{F}_{Ring/M}=k\frac{Q.\lambda'dz}{a^2+z^2}\cos{\theta}.\vec{u_z}$$ then substitute the cosine with $\frac{z}{\sqrt{a^2+z^2}}$ and so $$\vec{F}_{Ring/OA} = kQ\lambda'\int_0^a \frac{z.dz}{(a^2+z^2)^{3/2}}\vec{u_z}$$
I guess that's it, thank you!

 

[archaic]

What made me rethink using the cosine here is the fact that we're given the total charge of the ring, in my mind I was literally picturing myself looking from "a charge on the ring" point of view and I was imagining lines from all the other charges, as well as the one I'm looking from, moving towards a point M and naturally the electric field at that point was in the $\vec{u_z}$ direction, so I thought maybe we ought to directly express the field as $E=k\frac{Q}{a^2+z^2}\vec{u_z}$