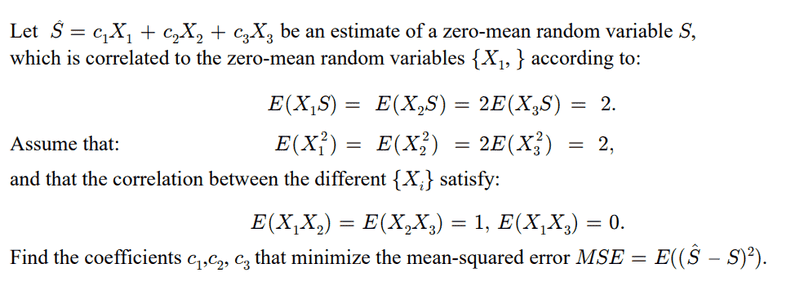SUMMARY
The discussion focuses on the Mean Squared Error (MSE) estimation for linear prediction involving a zero-mean random variable. The initial approach presented was deemed incorrect due to the improper assumption that the expected value of the estimate, ##\hat S##, equates to the actual value, ##S##. Instead, the correct method involves substituting ##\sum c_i X_i## for ##\hat S## in the expression for MSE, leading to a numerical minimization that yields coefficients approximately equal to 1 for two variables and near 0 for one. The possibility of an analytical solution for the optimization was acknowledged but not pursued.
PREREQUISITES
- Understanding of Mean Squared Error (MSE) estimation
- Familiarity with linear prediction models
- Knowledge of random variables and their properties
- Experience with numerical optimization techniques
NEXT STEPS
- Study the derivation of MSE in linear regression contexts
- Explore numerical optimization methods for coefficient estimation
- Learn about the properties of zero-mean random variables
- Investigate analytical solutions for MSE minimization problems
USEFUL FOR
Statisticians, data scientists, and machine learning practitioners involved in predictive modeling and MSE optimization will benefit from this discussion.