Multiple Transformations of Functions

In summary, the conversation discusses transforming the function f(x)=x^3 to a new function by finding the shifts and combining them. The resulting function is f(x) = a(x-3)^3 + 1, where a is the constant causing the stretch. The point (4,1.5) can be used to determine the value of a.
  • #1
saucybadimo
1
0
View attachment 9341

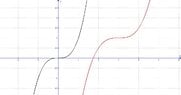
I have to transform the first function which is f(x)=x^3 to the second function. First, I have to find each shift then combine those to make a new function equation. I've used desmos and I know that there is a horizontal shift 3 units to the right. There is a vertical shift up but I don't know how many units. And I believe there is a stretch. There are only 3 transformations. PLEASE HELP!
 

Attachments

  • Screen Shot 2019-11-04 at 8.42.05 AM.png
    Screen Shot 2019-11-04 at 8.42.05 AM.png
    21.8 KB · Views: 54
Mathematics news on Phys.org
  • #2
note the function center point $(0,0)$ is translated to $(3,1)$, a horizontal shift right 3 units and a vertical shift up 1 unit.

taking into account the horizontal & vertical shifts, we have ...

$f(x) = a(x-3)^3 + 1$

... where $a$ is the constant causing the stretch

using the point $(4,1.5)$, can you determine the value of $a$ ?
 

Attachments

  • cubic_transformation.jpg
    cubic_transformation.jpg
    47.3 KB · Views: 53

1. What are multiple transformations of functions?

Multiple transformations of functions refer to the process of applying more than one transformation to a basic function, such as a linear or quadratic function. These transformations can include shifting, stretching, or reflecting the function's graph.

2. What is the order of transformations in a function?

The order of transformations in a function follows the acronym "SRF", which stands for shift, reflect, and stretch. This means that the function's graph will first be shifted, then reflected, and finally stretched or compressed.

3. How do I determine the effects of multiple transformations on a function?

To determine the effects of multiple transformations on a function, you can use the "inside-out" method. This involves starting from the innermost transformation and working your way outwards, keeping track of each transformation's effect on the function's graph.

4. Can multiple transformations be applied to any type of function?

Yes, multiple transformations can be applied to any type of function, as long as it is a basic function with a defined graph. This includes linear, quadratic, exponential, and trigonometric functions.

5. How do I graph a function with multiple transformations?

To graph a function with multiple transformations, you can use the "transformed parent function" approach. This involves graphing the basic function first, and then applying each transformation one by one to the graph. Alternatively, you can use a graphing calculator or software to graph the function automatically.

Similar threads

I Transformation of Functions: How Do Domain and Range Change?
    • General Math
Replies
4
Views
902
B Correlation between shifting graph of a function and shifting the axes
    • General Math
Replies
5
Views
1K
I Moving center of coordinates in the polar graph
    • General Math
Replies
2
Views
1K
MHB Pre-calculus Grade 11 IB (higher level)
    • General Math
Replies
2
Views
1K
MHB The shifting of h in vertex form
    • General Math
Replies
1
Views
1K
A Memory issues in numerical integration of oscillatory function
    • General Math
Replies
3
Views
448
I Can the same argument be used for both radians and degrees in the sine function?
    • General Math
Replies
3
Views
764
I Calculating the inverse of a function involving the error function
    • General Math
Replies
3
Views
226
I Get the time axis right in an inverse Fast Fourier Transform
    • General Math
Replies
2
Views
2K
I Name of distance to nearest multiple of n function?
    • General Math
Replies
1
Views
664

Hot Threads

Recent Insights

Back
Top