Multivariable limits - path problem

[WonderKitten]

TL;DR Summary

What path could I use to prove that the following limit doesn't exist.

Hey, so I have the following problem:

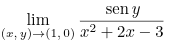
I'm trying to prove that the limit doesn't exist (although I'm not sure if it does or not) so:
along y=mx -> x=y/m:

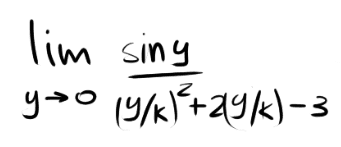, which is 0 for all k≠0.
along y^n it's the same and I'm not sure what I should do next. Could I set x = sin(y)?
If I can, then the limit in that instance would be infinite, thus proving that the limit doesn't exist, right?

 

[mathman]

You cannot use $y=mx$ since it is inconsistent with $y\to 0$ and $x\to 1$. You might try $y=m(x-1)$.

 

[Delta2]

I also suggest along @mathman advice to factorize the denominator as $(x-1)(x+3)$.

 

[FactChecker]

You know that for $y$ restricted to $-1<y<1$ and $x$ sufficiently near 1 (edited, was 0, which is wrong), there are values of $y$ where $\sin(y) = x^2+2x-3$ and other values for $y$ where $\sin(y) = 2(x^2+2x-3)$. Those $y$ values go to zero as $x$ goes to 1 and give two different constant values, 1 and 2, for the ratio.

EDIT: I had x going to the wrong value, 0, when it should have been going to 1.