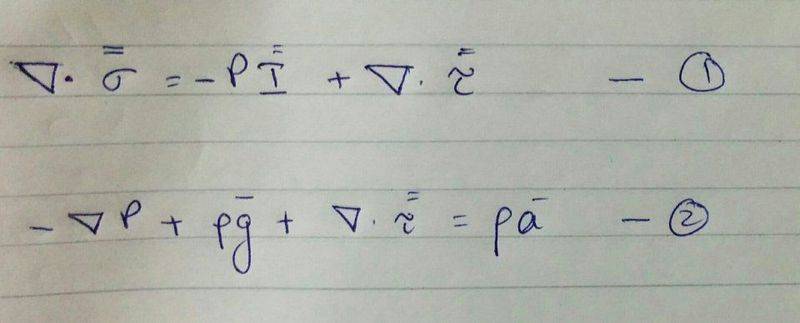SUMMARY
The discussion focuses on the derivation of the Navier-Stokes Equations for constant density and viscosity, specifically addressing a potential error in the derivation presented by Roger Rangel. The first equation, representing the stress tensor, is given as $$\vec{σ}=-P\vec{I}+\vec{τ}$$, while the second equation is the momentum balance equation $$∇\centerdot \vec{σ}+ρ\vec{g}=ρ\vec{a}$$. Participants emphasize the importance of correctly applying the divergence of the stress tensor and note that the constant density assumption does not account for temperature and volume effects. The book "Transport Phenomena" by Bird, Stewart, and Lightfoot is recommended for further study.
PREREQUISITES
- Understanding of the Navier-Stokes Equations
- Familiarity with tensor notation and manipulation
- Knowledge of fluid mechanics principles
- Basic concepts of stress and strain in fluids
NEXT STEPS
- Study the derivation of the Navier-Stokes Equations in detail
- Learn about the application of dyadic tensor notation in fluid mechanics
- Explore the impact of temperature and volume changes on fluid density
- Read "Transport Phenomena" by Bird, Stewart, and Lightfoot for comprehensive fluid mechanics knowledge
USEFUL FOR
Students and professionals in fluid mechanics, engineers working with fluid dynamics, and anyone seeking to deepen their understanding of the mathematical foundations of the Navier-Stokes Equations.