- #1
Gohar Shoukat
- 8
- 1
I was watching a lecture in which the professor derived the Navier Stokes Equations for const density and viscosity. He however skipped a step and directly went from one equation to another without giving any explanation. I have attached an image file in which the 2nd equation is derived from the first equation. Can anyone please explain how this came to be?
I apologize in advance for uploading a handwritten equation.
oh 'I' in the image below is the identity matrix
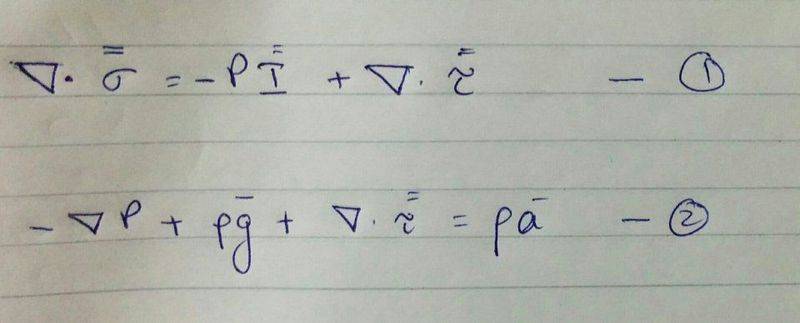
I apologize in advance for uploading a handwritten equation.
oh 'I' in the image below is the identity matrix