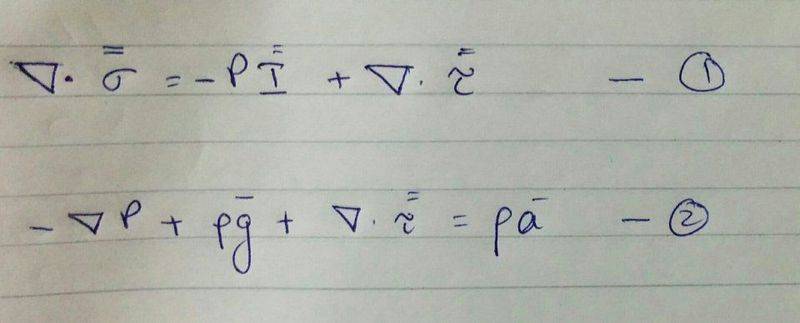Discussion Overview
The discussion revolves around the derivation of the Navier-Stokes equations for fluids with constant density and viscosity. Participants seek clarification on the steps involved in the derivation, particularly regarding the transition between two equations presented in a lecture. The conversation includes technical explanations, challenges to the correctness of the equations, and inquiries about resources for further study in fluid mechanics.
Discussion Character
- Technical explanation
- Debate/contested
- Homework-related
- Mathematical reasoning
- Meta-discussion
Main Points Raised
- One participant requests clarification on a skipped step in the derivation of the Navier-Stokes equations, specifically how one equation transitions to another.
- Another participant explains that the first equation represents molecular stress, which includes pressure and viscous stress, and discusses the role of the identity matrix in this context.
- Some participants assert that the first equation is incorrect, claiming that a divergence operator should be included in front of the pressure term.
- There is a challenge regarding the dimensional consistency of the terms in the equations presented by Roger Rangel, with some participants suggesting that the derivation should yield different results.
- Several participants recommend the book "Transport Phenomena" by Bird, Stewart, and Lightfoot as a resource for understanding the mathematics involved in fluid mechanics, noting its strengths and some unconventional aspects of its notation.
- One participant expresses a desire for a comprehensive resource on fluid mechanics that covers more than just tensor notation.
Areas of Agreement / Disagreement
Participants express disagreement regarding the correctness of the first equation and the necessity of including a divergence operator. There is no consensus on the validity of the equations presented, and multiple competing views remain regarding the derivation process.
Contextual Notes
Some participants note that the term "constant density" implies that density does not change due to pressure variations, but may still vary with temperature and volume effects. There are also mentions of unconventional sign conventions in the recommended textbook that may affect understanding.
Who May Find This Useful
This discussion may be useful for students and professionals interested in fluid mechanics, particularly those seeking clarification on the Navier-Stokes equations and recommendations for educational resources in the field.