Karmann
- 1
- 0
- TL;DR
- Calculating maximum stress in a bolted assembly
Trying to calculate the maximum stress that would occur in the attached assembly...
The assembly consists of a tube sandwiched between two plates that are bolted down to a larger plate with an M6 bolt. Each of the two plates have a 400N force acting on them which is perpendicular to the axis of the bolt. The M6 bolted is tightened to 9Nm, generating a clamping force of around 7500N.
I believe the location of maximum (tensile) stress would occur in the position marked by the red dot due to the bending moment created around rotation axis (green dot).
Thanks
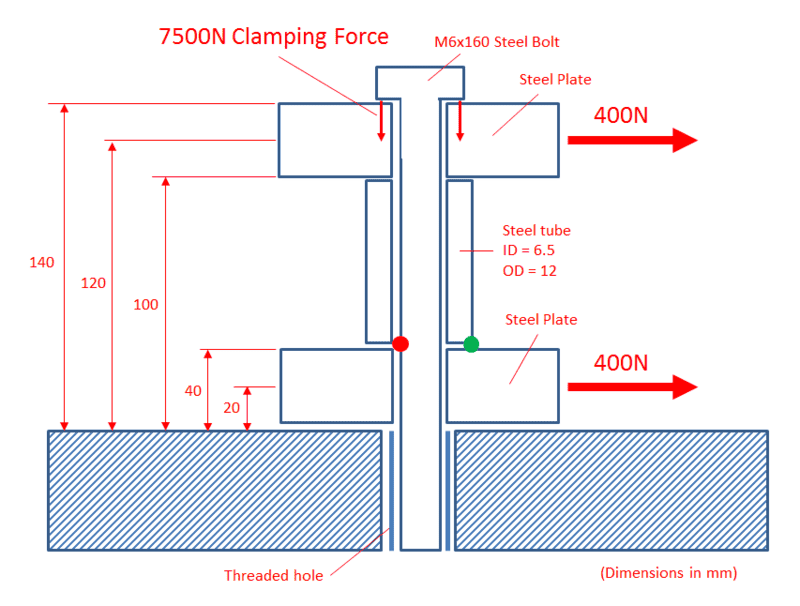
The assembly consists of a tube sandwiched between two plates that are bolted down to a larger plate with an M6 bolt. Each of the two plates have a 400N force acting on them which is perpendicular to the axis of the bolt. The M6 bolted is tightened to 9Nm, generating a clamping force of around 7500N.
I believe the location of maximum (tensile) stress would occur in the position marked by the red dot due to the bending moment created around rotation axis (green dot).
Thanks
Last edited by a moderator: