X8V
- 2
- 0
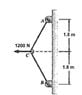
Knowing that portions AC and BC of cable ACB must be equal, determine the shortest length of cable that can be used to support the load shown if the tension in the cable is not to exceed 870 N.
i attached the picture that came with the problem.
i am lost and not sure how to approach the problem.
i attached the picture that came with the problem.
i am lost and not sure how to approach the problem.