- #1
Prathamesh
- 20
- 1
Homework Statement
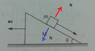
All the surfaces shown in fig. are assumed to be frictionless. The block of mass m slides on the prism of mass M which in turn slides backwards on horizontal surface with acceleration of ao. Find the acceleration of smaller block with respect to prism.
Homework Equations
The Attempt at a Solution
As we are working from the frame of reference of prism which is non inertial
we have to include a pseudo force in opp. direction of acc of prism.
Now , forces on the block are
1)mg downwards
2)Normal force N
3)pseudo force (mao)
When I resolved these forces using force body diagram , it gave me 2 equations
maocosθ+mgsinθ=ma
i.e aocosθ+gsinθ=a
and
N+maosinθ=mgcosθ
I m stuck here...
How to eliminate N and ao ??
Please help
Ans is
(M+m)gsinθ / M + msin2θ
Last edited by a moderator: