B Newton's Third Law in space

[LloydGarmadon]

Newton's Third Law states that forces occur in pairs of equal magnitude acting in opposite directions on opposing bodies. When we push against a wall, the wall pushes back with a force of equal magnitude and we move as a result of not being inert enough. What would the force pair be if an astronaut pushes against nothingness in space? Is the reaction pair within the body, and the fist accelerates orders of magnitude more noticeable than the body due to difference in inertia?

 

[Nugatory]

Is the reaction pair within the body, and the fist accelerates orders of magnitude more noticeable than the body due to difference in inertia?

yes, so the body moves a little bit in one direction, the fist moves a lot more in the other direction, and the center of mass of the astronaut doesn’t move at all. If they’re floating stranded ten meters from the hatch of their spaceship they’re as helpless as if it were ten thousand kilometers - no way of moving themself through space.

 

[LloydGarmadon]

@Nugatory Thanks for the kind help. If we apply this understanding on earth, say punching a wall, your centre of mass remains stationary until the punch reaches the wall and the reaction force pushes you backwards... and a net force is only created when you apply some of that force/momentum of the wall to have it back at you.. If thats the case, can it be qualitatively understood by: say we have numbers representing "units" of forces. before you touch the wall, its -10 vs 10, centre of mass no movement, but when you hit the wall, some of that action goes to the wall and the wall pushes you, which results is -10 + -5 vs 5, hence generating a net force?

 

[berkeman]

No, you are overthinking this. At every instant of time, if you are in a frictionless environment, your center of mass position is constant. So if you are on a frictionless sheet of ice and move your body or push a heavy dumbbell to the side, the center of mass of you and <whatever> stays in the same position.

 

[Nugatory]

and a net force is only created when you apply some of that force/momentum of the wall to have it back at you

It’s easier to think about these problems if we consider the wall to have infinite mass; no matter what force we apply to it its acceleration is zero so it never moves. (This is a really good approximation when the wall is rigidly attached to the planet earth…. a worthwhile exercise would be to calculate just how good the approximation is for reasonable assumptions about your weight and strength).

With that assumption, when you are pushing on the wall we have three things each subject to their own forces:
- the wall, which is subject to a force from the hand pushing on it.
- the hand, which is subject to the third-law equal and opposite force from the wall and also to the force from your body pushing on it.
- your body, which is subject to the third-law equal and opposite force from the hand.

The wall doesn’t move, by assumption.
The hand doesn’t move because the net force on it is zero - the forces on it cancel.
Your body is subject to the non-zero force from the hand, so it moves,

It’s often best to think of these problems by drawing what’s called a “free body diagram”, Google will find some good descriptions.

If thats the case, can it be qualitatively understood by: say we have numbers representing "units" of forces. before you touch the wall, its -10 vs 10, centre of mass no movement, but when you hit the wall, some of that action goes to the wall and the wall pushes you, which results is -10 + -5 vs 5, hence generating a net force?

Much better to think in terms of $F=ma$. When the wall is not there to provide an opposing force your hand will accelerate away from you, you won’t be able to keep applying that force unless your arm can keep up and there’s only so fast that it can move. So there’s only so much acceleration possible and hence a limit on how much force you can apply to the hand.

 

[A.T.]

If we apply this understanding on earth, say punching a wall, your centre of mass remains stationary until the punch reaches the wall ...

Only if you are standing on a frictionless surface.

 

[sophiecentaur]

Is the reaction pair within the body

There is nothin to push against so the "pair" of forces would both be zero. There are plenty of forces going on inside the body as the muscles accelerate limbs etc but they are hard to identify in detail. With a hanging chain, each link - link pair will have a N3 pair and the pairs will have increasing magnitude as you look higher up the chain and smaller as you go down. The 'N3 pair' at the very bottom surface of the bottom link will be zero-zero (Newton works over the whole chain).

 

[L Drago]

According to Newton's third law, every action has an equal and opposite reaction.

For this reason, we can sit on a chair as we exerrt force on chair and chair exerts equal and opposite force on us or it will collapse. I think it can be represented by this equation

F action - - - - - - > F reaction.

This is the reason Rockets are able to launch from Earth due to action reaction force.

I am a seventh grader so kindly explain me where I am getting it wrong.

 

[L Drago]

Newton's Third Law states that forces occur in pairs of equal magnitude acting in opposite directions on opposing bodies. When we push against a wall, the wall pushes back with a force of equal magnitude and we move as a result of not being inert enough. What would the force pair be if an astronaut pushes against nothingness in space? Is the reaction pair within the body, and the fist accelerates orders of magnitude more noticeable than the body due to difference in inertia?

The rest of our body might react and feel an equal and opposite force. Space has no air resistance. Hence, our body can move backwards to conserve the momentum.It is my opinion on this matter as Newton's third law must work everywhere.

 

[sophiecentaur]

This is the reason Rockets are able to launch from Earth due to action reaction force.

....or in empty space. The reaction force pairs are in the rocket engine - pushing out the propellant and pushing the rocket forward.

 

[blue raven]

Nobody tells you that there are big differences. You can push an object either with straight arms, accelerating towards it, or with bend arms. The awkward thing is that in the first case Reaction will only decelerate you, while in the second case Reaction will move you backwards. This difference is given by the fact that in the first case Reaction is given by Inertia, while in the second case Reaction is given by elastic forces.

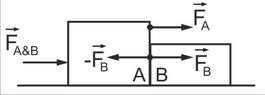
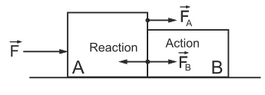
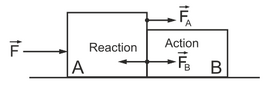
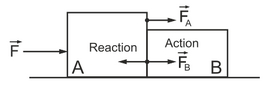
When you push an object with straight arms, accelerating towards it, see the image below, then the math is very simple and clear, given by either Composition of Forces (Vectors) or the Second Law.

Here is the simple math using Composition of Forces. When object A pushes object B, both objects are accelerated by the same force F which is divided into the two forces that accelerate each object
$$F=F_{A}+F_{B}.$$
Action is the force FB that accelerates object B, Reaction is the force that decelerates object A. We can calculate the force that accelerates (only) object A
$$F_{A}=F-F_{B}$$
So from this equation we can see that object A will always be decelerated by a force $-F_{B}$ which we defined as Reaction. Thus Action=-Reaction, or from the above image $F_{B}=-(-F_{B})$.

When you push with your arms bent, in this case you and whatever you are pushing will be accelerated by elastic forces, in which case Hooke's Law, $F=-kx$, applies, which says that the elastic force is given by the distance x by which the spring restores its length. Below is the case when the two bodies at the ends of the spring have equal mass.

By the way this distance x is a vector, it has magnitude and most importantly direction, so that the Hooke's Law is correctly written as
$$\vec{F}=-k\vec{x}$$
So, after measuring the distances/vectors $x_{1}$ and $x_{2}$ by which you restore the arm length in both directions, you can calculate the opposite elastic forces.
Also, knowing the distances traveled by the two bodies, you can use the kinematic eq
$$d=\dfrac{at^2}{2}$$
to calculate both accelerations, and then both opposite forces given by the Second Law $F=ma$.
Both mathematical calculations are interesting, but are actually forbidden by forum rules, because there are no such mathematical calculations in any textbooks anywhere in the world, so I can't help you with that.
PS
I have no idea how to insert LaTeX here (solved by admin, thanks!).

 

[berkeman]

I have no idea how to insert LaTeX here.

I'll send you a PM with tips...

 

[sophiecentaur]

Nobody tells you that there are big differences. You can push an object either with straight arms, accelerating towards it, or with bend arms. The awkward thing is that in the first case Reaction will only decelerate you, while in the second case Reaction will move you backwards.

There are no "big differences" in the principles involved. The basic rules in Newtonian Mechanics apply in the same way for all such problems.

because there are no such mathematical calculations in any textbooks anywhere in the world

What evidence of that do you have? In the hundreds of years that Newtonian Mechanics has been studied by thousands (millions?) of people your particular question has surely been dealt with in some form or another. Where is the specific hole in Mechanics that has failed to be studied enough to satisfy you? There is nothing here that can't be dealt with within the rules of PF. If you feel that you are following some forbidden path then you can apply the 'rules' to each step in your reasoning. If the answer you get is wrong it will be due to some error in your Maths and not because you have found a gap in Physics.

So from this equation we can see that object A will always be decelerated by a force −FB which we defined as Reaction.

Using the word 'decelerated' is risky in an argument. You can avoid a lot of confusion if you just use positive or negative acceleration in your Maths. Constructing a proper Free Body Diagram can be difficult and intuition alone can lead to errors.

 

[blue raven]

There are no "big differences" in the principles involved. The basic rules in Newtonian Mechanics apply in the same way for all such problems.

I wrote that clear, in one case Reaction is provided by Inertia, in the second case is provided by elastic forces. There are big differences between Inertia and elastic forces I think, maybe you do not.

What evidence of that do you have? In the hundreds of years that Newtonian Mechanics has been studied by thousands (millions?) of people your particular question has surely been dealt with in some form or another. Where is the specific hole in Mechanics that has failed to be studied enough to satisfy you? There is nothing here that can't be dealt with within the rules of PF.

I wrote very clearly, there are no such mathematical calculations neither in textbooks nor on the internet. If you know that such mathematical calculations exist somewhere, you can put them here, I don't mind. The only math calculation that proves Newton's Third Law is for two bodies that accelerate in the same direction. Such an example can be found here, by Walter Lewin
Anyone can see that even Walter Lewin did not prove this law for the part in which bodies accelerate by moving in opposite directions, which is the case of two bodies accelerated by a spring.
Since there is no such mathematical calculation in the textbooks, I am not willing to expose it here because it is forbidden by the forum rules, which I don't mind, it is for the safety of the students, I get it.
One of our major "markets" is high-school and university students who use us to help them understand the material that they are studying.
https://www.physicsforums.com/threa...w-tos-for-physics-forums.617567/#post-4664231
This math is not in textbooks, and I'm not here (as long as I stay) to break the forum rules, period.

 

[sophiecentaur]

This math is not in textbooks, and I'm not here (as long as I stay) to break the forum rules, period.

Which particular Maths isn't there. One experiment you could do would be to show us your Maths and see what the Mods do about it. What harm are you suggesting that the students might suffer?

even Walter Lewin did not prove this law

He actually said that the law can't be proved; it's just universally demonstrated experimentally. So you are using that video as and argument in favour of your idea but it doesn't try to prove anything - in particular, it doesn't even mention your 'top secret' idea. Where could this thread possibly go now?

Are you for real or this thread just nonsense? (Some evidence could be useful here)

 

[weirdoguy]

@blue raven I don't think you grasped that physics is an experimental science, and there some things that can't be proven mathematically. And your attitude is a little bit misplaced.

 

[sophiecentaur]

@blue raven I don't think you grasped that physics is an experimental science, and there some things that can't be proven mathematically. And your attitude is a little bit misplaced.

The OP doesn't actually have a thesis here and offers no evidence about this 'forbidden' stuff. We're only a hair's breadth from a 'conspiracy'.

 

[berkeman]

The OP doesn't actually have a thesis here and offers no evidence about this 'forbidden' stuff. We're only a hair's breadth from a 'conspiracy'.

Technically they are not the OP, since they revived the thread in post #11. But yeah, this thread may get closed and pruned sometime soon.

 

[blue raven]

My first post shows how to calculate mathematically (why no one did that?) the opposite forces, Action-Reaction, in two different scenarios
1. When someone accelerates towards an object, pushing it with straight hands
2. When someone pushes an object with bent hands

1. In the first case, Reaction on the guy is produced by Inertia, and can be mathematically calculated/proved, as in the above video by Walter Lewin, using the Second Law, or as I did my self above using Composition of Forces.
2. In the second case, Reaction is produced by the elastic forces, and the opposite forces Action and Reaction can be mathematically calculated using either the Hooke's Law, $F=-kx$, or using the kinematic equation $d=\dfrac{at^2}{2}$ which gives both accelerations, which gives further the opposite forces $F=ma$.
The only math that exists in textbooks or on the internet, is the one performed by Walter Lewin, which is the first scenario. That is it, no more.
It seems that performing math and presenting diagrams, I intended to commit a crime. Seriously?
Good day!

 

[berkeman]

It seems that performing math and presenting diagrams, I intended to commit a crime. Seriously?

Thread is closed temporarily for Moderation and crime fighting...

 

[berkeman]

Thread will remain closed.