NFA Hello! (Wave) - Computation Theory Explanation

[evinda]

Hello! (Wave)

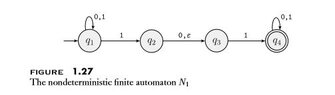
According to the book of Michael Sipser: Introduction to the Theory of Computation we have the following:

View attachment 5733

View attachment 5735

Could you explain to me why after having read the first 0, we can go to state $q_3$ ?

I have drawn the tree and I find also an other result after having read the second 1.

That's what I get:

View attachment 5734

What am I doing wrong?

 

[Evgeny.Makarov]

Could you explain to me why after having read the first 0, we can go to state $q_3$ ?

The automata goes to $q_3$ (amontg other states) after reading 01. This is because after reading 1 it arrives in state $q_2$ and then it does an $\varepsilon$-transition to $q_3$ without reading any symbol.

 

[I like Serena]

Hey evinda! (Smile)

Could you explain to me why after having read the first 0, we can go to state $q_3$ ?

Isn't that after reading $0, 1, \varepsilon$ instead of just $0$? (Wondering)

EDIT: Ah, I only see just now that Evgeny beat me to it.

I have drawn the tree and I find also an other result after having read the second 1.

That's what I get:

What am I doing wrong?

Well... I don't see a state transition from $q_2$ to $q_2$ while reading $1$.

 

[evinda]

I am confused right now. According to the tree of the book, we are at the beginning at state $q_1$, then in order to read $0$ the automata goes to $q_1$ and then in order to read $1$ it could go to states $q_1, q_2, q_3$.

But we can go to state $q_3$ after having read $1$. So shouldn't $q_3$ be at the third line and not at the second one?

Or am I wrong?

 

[Evgeny.Makarov]

But we can go to state $q_3$ after having read $1$. So shouldn't $q_3$ be at the third line and not at the second one?

It's not clear what you mean by "line". If you mean "a row of states in the picture of a tree in post #1", then $q_3$ is indeed in line 3. Both line 1 and line 2 consist of a single state $q_1$.

 

[evinda]

It's not clear what you mean by "line". If you mean "a row of states in the picture of a tree in post #1", then $q_3$ is indeed in line 3. Both line 1 and line 2 consist of a single state $q_1$.

Yes, by line I meant "a row of states in the picture of a tree in post #1".
And I started counting after the starting state, because we go to this without reading a symbol.
So if we incude the starting state, at the first line we have it.
Then the automata goes again to $q_1$ in order to read $0$. So at the second line, we have $q_1$.
Then we want to read $1$. So there are two possibilities for the automata: to go to state $q_1$ or to $q_2$.
So at the third line we have the states $q_1$ and $q_2$. Or am I wrong?

 

[Evgeny.Makarov]

Then we want to read $1$. So there are two possibilities for the automata: to go to state $q_1$ or to $q_2$.
So at the third line we have the states $q_1$ and $q_2$.

This has already been addressed.

The automata goes to $q_3$ (among other states) after reading 01. This is because after reading 1 it arrives in state $q_2$ and then it does an $\varepsilon$-transition to $q_3$ without reading any symbol.

The design of the tree is such that line $k$ ($k=1,2,\dots$) includes all states where the automaton can arrive after reading the first $k-1$ symbols of the word 010110. Note that this does not mean "after $k-1$ transitions along arrows". After reading 01 the automaton can end up in state $q_2$ and then without reading anything it can go to $q_3$. Thus, after reading 01 it can arrive in $q_3$. Therefore $q_3$ is in line 3.

 

[evinda]

The design of the tree is such that line $k$ ($k=1,2,\dots$) includes all states where the automaton can arrive after reading the first $k-1$ symbols of the word 010110. Note that this does not mean "after $k-1$ transitions along arrows". After reading 01 the automaton can end up in state $q_2$ and then without reading anything it can go to $q_3$. Thus, after reading 01 it can arrive in $q_3$. Therefore $q_3$ is in line 3.

Ok, I got it now.

If we want to read the symbol $1$, can we first do an $\epsilon$-transition and then read it?

Or is it only allowed to read first $1$ and then do an $\epsilon$-transition?

 

[Evgeny.Makarov]

If we want to read the symbol $1$, can we first do an $\epsilon$-transition and then read it?

Or is it only allowed to read first $1$ and then do an $\epsilon$-transition?

From which state? If you mean from $q_1$, is there an outgoing $\varepsilon$ arrow from that state?

I recommend reading the definition carefully. It may save you many questions.

 

[evinda]

From which state? If you mean from $q_1$, is there an outgoing $\varepsilon$ arrow from that state?

I was wondering if after having read 0101 and we are at state $2$, we can do an $\epsilon$-transition and then read $1$.

 

[I like Serena]

I was wondering if after having read 0101 and we are at state $2$, we can do an $\epsilon$-transition and then read $1$.

Yep. We can. It corresponds with the transition to $q_3$ followed by the transition to $q_4$ in diagram $1.27$. (Nod)

 

[evinda]

Yep. We can. It corresponds with the transition to $q_3$ followed by the transition to $q_4$ in diagram $1.27$. (Nod)

Ah I see... Thank you very much! (Smile)

- - - Updated - - -

The design of the tree is such that line $k$ ($k=1,2,\dots$) includes all states where the automaton can arrive after reading the first $k-1$ symbols of the word 010110. Note that this does not mean "after $k-1$ transitions along arrows". After reading 01 the automaton can end up in state $q_2$ and then without reading anything it can go to $q_3$. Thus, after reading 01 it can arrive in $q_3$. Therefore $q_3$ is in line 3.

Thanks a lot! (Smirk)