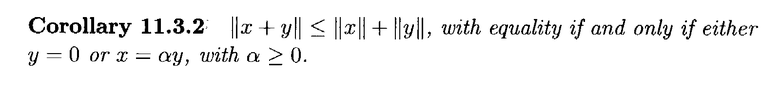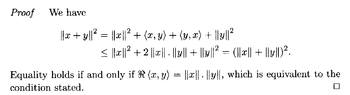Normed and Inner Product Spaces .... Garling, Corollary 11.3.2 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help to fully understand the proof of Corollary 11.3.2 ... (Corollary to the Cauchy-Schwarz Inequality ... )

Garling's statement and proof of Corollary 11.3.2 reads as follows:View attachment 8960
View attachment 8961In the above text from Garling we read the following:

" ... ... Equality holds if and only if $$\mathscr{R} \ \langle x, y \rangle = \| x \| . \| y \|$$, which is equivalent to the condition stated. ... ... "
Can someone please rigorously demonstrate that the condition that ... $$\mathscr{R} \ \langle x, y \rangle = \| x \| . \| y \| $$ ...

... is equivalent to ... either $$y = 0$$ or $$x = \alpha y$$ with $$\alpha \ge 0$$ ... ...Help will be appreciated ...

Peter

 

[Opalg]

Can someone please rigorously demonstrate that the condition that ... $$\mathscr{R} \ \langle x, y \rangle = \| x \| . \| y \| $$ ...

... is equivalent to ... either $$y = 0$$ or $$x = \alpha y$$ with $$\alpha \ge 0$$ ... ...

${\frak R}\langle x,y\rangle \leqslant |\langle x,y\rangle| \leqslant \|x\|\|y\|$, and (by Cauchy-Schwarz) equality can only hold in the second of those inequalities if $x$ and $y$ are linearly dependent. In that case, either $y$ is zero or $x$ must be a scalar multiple of $y$.

To see that $\alpha \geqslant0$, if $x = \alpha y$ then $\langle x,y\rangle = \langle \alpha y,y\rangle = \alpha \|y\|^2$. Also, $\|x\|\|y\| = |\alpha|\|y\|^2$. So if ${\frak R}\langle x,y\rangle = \|x\|\|y\|$ (and $y\ne0$) it follows that ${\frak R}\alpha = |\alpha|$. For a complex number $\alpha$, that implies that $\alpha$ is real and non-negative.

 

[soloenergy]

Sure, I can try to help explain this for you. First, let's break down the statement and proof of Corollary 11.3.2. The corollary is a result that follows from the Cauchy-Schwarz Inequality, which states that for any two vectors x and y in a normed space, we have:

| \langle x, y \rangle | \le \| x \| \cdot \| y \|

with equality holding if and only if x and y are linearly dependent. This means that either x = \alpha y or y = \alpha x for some scalar \alpha.

Now, let's look at Garling's statement and proof. He says that equality in the Cauchy-Schwarz Inequality holds if and only if \mathscr{R} \ \langle x, y \rangle = \| x \| \cdot \| y \|, which is equivalent to the condition stated. This condition is that either y = 0 or x = \alpha y with \alpha \ge 0.

To see why this is true, we can consider two cases.

Case 1: y = 0. In this case, it is clear that \mathscr{R} \ \langle x, y \rangle = \| x \| \cdot \| y \|, since both sides are equal to 0.

Case 2: y \neq 0. In this case, we can write y as a scalar multiple of x, i.e. y = \alpha x for some scalar \alpha. Then, we have:

\mathscr{R} \ \langle x, y \rangle = \mathscr{R} \ \langle x, \alpha x \rangle = \alpha \mathscr{R} \ \langle x, x \rangle = \alpha \| x \|^2

On the other hand, \| x \| \cdot \| y \| = \| x \| \cdot \| \alpha x \| = \| x \| \cdot | \alpha | \| x \| = | \alpha | \| x \|^2

Since x \neq 0 (otherwise y would be 0), we have \| x \| \neq 0, which means that | \alpha | = \alpha. Therefore, we have:

\mathscr{R} \ \langle x, y \rangle = \| x \| \cdot \| y \| if and