Norton's Theorem with Dependent Sources?

[Master1022]

Homework Statement

Find the short circuit current and hence the Norton equivalent circuit.

Relevant Equations

V = IR

My question is: What is wrong with my working/ method (in the attached pictures) to find $i_{sc}$? I can get the Norton equivalent from there, but seem to get the same answer as the solution scheme.

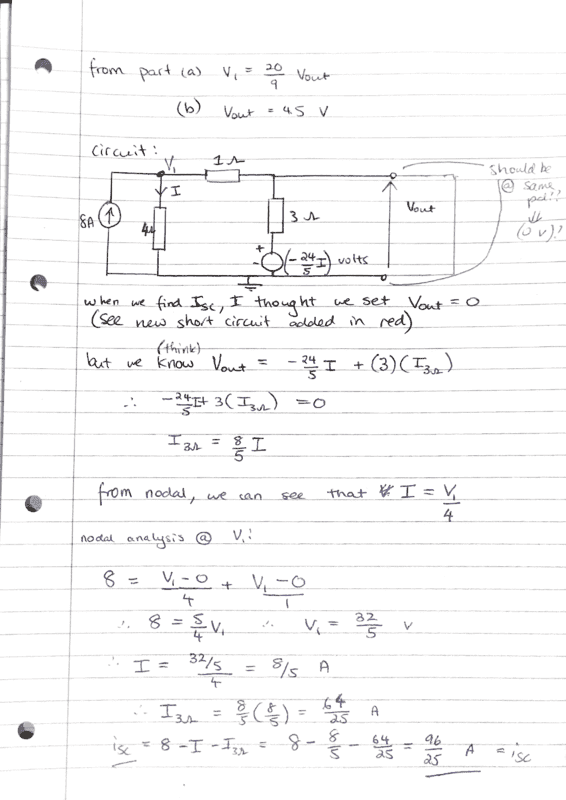
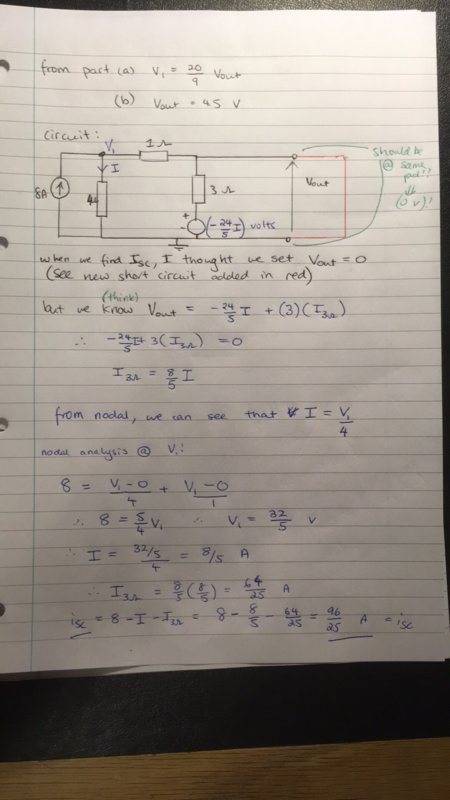
Context: we are given the circuit depicted in the picture (initially with no connection between the $V_{out}$ nodes) and the question is building up to us finding the Norton equivalent circuit. From the previous parts, we have shown:
- $V_1 = \frac{20}{9} V_{out}$ for the open circuit condition
- $V_{out} = 4.5$ Volts

The answer uses the method of setting the sources to 0, but we have been told (in lectures) that method is not valid when there are dependent current sources.

I have asked a peer and they suggested that the error may lie in the fact that I let $V_{out} = 0$ volts, but I cannot see why that is the error.

I have attached two versions of the working, but hopefully, it is legible.

I would appreciate any help.

 

[LeafNinja]

When doing Norton/Thevenin Equivalent circuits you need$i_{sc}$ (short circuit current) and $v_{oc}$(open circuit voltage). You correctly found $i_{sc}$ for the short/closed circuit as or 3.84 A.

.

If you solve the open circuit condition you will get $V_{out}$ =4.5 V. Then to get $R_{N}$, you simply use the equation:$$R_{N} =\frac{V_{oc}}{I_{sc}}=1.17\Omega$$

You seem to have everything right, so could you clarify why you believe you have an error.

Also, you can use superposition applying one independent source at a time. Treat the dependent sources as resistors and always leave them on.

​

 

[Master1022]

When doing Norton/Thevenin Equivalent circuits you need$i_{sc}$ (short circuit current) and $v_{oc}$(open circuit voltage). You correctly found $i_{sc}$ for the short/closed circuit as or 3.84 A.

.

If you solve the open circuit condition you will get $V_{out}$ =4.5 V. Then to get $R_{N}$, you simply use the equation:$$R_{N} =\frac{V_{oc}}{I_{sc}}=1.17\Omega$$

You seem to have everything right, so could you clarify why you believe you have an error.

Also, you can use superposition applying one independent source at a time. Treat the dependent sources as resistors and always leave them on.

​

Thank you for your response. The solution to the problem gets a different answer to me and it sets the sources to 0 (the shortcut method). However, I was previously led to believe that method only worked for independent sources.

EDIT: sorry, I just re-read my first post. It should say "cannot get the same answer as the solution scheme..."