- #1
priceofcarrot
- 32
- 0
Homework Statement
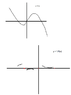
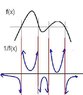
The y = f(x) is the original graph. The question asks me to draw the y = 1/f(x) of that graph. What I did was just use the same x coordinates and then take the y coordinates and just do 1/y coordinate for each y coordinate. Is this the correct way to do it?
Also, the red dots on the graph of the y = 1/f(x) are the areas of the graph that are undefined (meaning I couldn't do 1/y coordinate, because the y coordinate was 0). Does that mean that those points are asymptotes? If they are, how do I figure out if they're horizontal or vertical asymptotes?Also, you'll see that right before and after the red dots on the graph of y = 1/f(x) there is empty space. I wasn't sure if I was supposed to draw the lines of the graph up until the red dots (the asymptotes if that is what they represent), or just until the points that were available to me (the ones that I got from the original graph and then did 1/by the y coordinates).Thanks
EDIT: Those aren't my final graphs. They're just quick drawings to illustrate what I'm talking about.