Not sure what square brackets indicate when dealing with partial derivates

[Kushwoho44]

Hi guys, attached is a picture of my problem and it is also underlined.

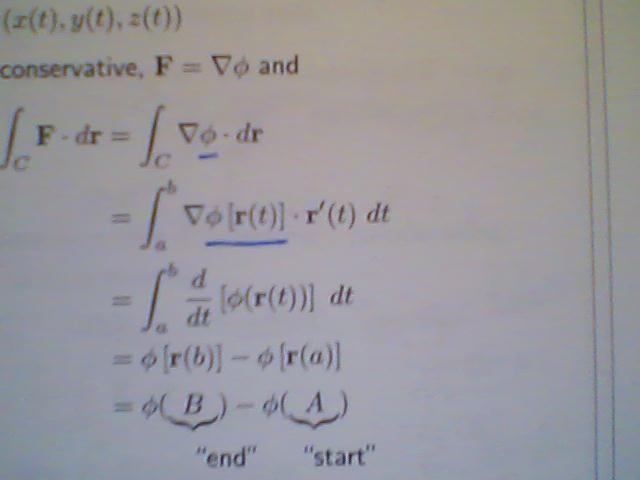
I've been reading through this theory and I just don't understand what the square brackets indicate.

I understand that ∇phi is the partial derivative with respect to the scalar function phi.

But what is ∇phi [r(t)] ?

I feel ashamed asking this like I'm going to be laughed at.

 

[Simon Bridge]

$\nabla\phi$ is the the gradient of $\phi$: it is read "grad phi" or "del phi".
So it involved taking the partial derivative of phi with respect to each coordinate axis.
http://en.wikipedia.org/wiki/Gradient

$\phi[\vec{r}(t)]$ is just telling you that $\phi$ is a function of $\vec{r}$ which, in turn, is a function of $t$. What they've done is parameterized the path represented by the C. Having turned $\phi$ into a function of just one variable, the gradient is much simplified.

 

[HallsofIvy]

They are just using "[ ]" in place of "( )" because they are already using "( )" for the "$\vec{r}(t)$" and don't want to have "))". There is no difference in meaning.