SUMMARY
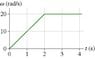
The discussion focuses on calculating the number of revolutions an object makes in the first 4 seconds based on its angular velocity graph. The correct approach involves finding the area under the angular velocity vs. time graph to determine angular displacement. The calculated angular displacement is 60 radians, leading to approximately 9.55 revolutions when divided by 2π. Key insights include the importance of understanding the relationship between angular velocity, time, and angular displacement.
PREREQUISITES
- Understanding of angular velocity and its units (rad/s)
- Familiarity with graph interpretation, specifically area under curves
- Knowledge of angular displacement and its relationship to revolutions
- Basic calculus concepts related to integration of functions
NEXT STEPS
- Study the concept of angular displacement and its calculation from velocity graphs
- Learn about the integration of functions to find areas under curves
- Explore the relationship between angular velocity and linear motion
- Investigate the applications of angular motion in physics problems
USEFUL FOR
Students studying physics, particularly those focusing on rotational motion, as well as educators looking for effective methods to teach angular displacement and velocity concepts.