High School Object A is moving relative to O , what does it mean?

[diazdaiz]

since i am new at learning special relativity, i still miss the concept about how thing move in special relativity. In high school, i am doing several problem about velocity addition, and that word always appear. for example:
A is moving with velocity v_AO relative to O, and B is moving with velocity v_BO relative to O, what is A velocity relative to B?
and then i am using formula
V_AB=(V_AO+V_OB)/(1+V_AO.V_OB/c²)
and then you get the answer
but i can't really understand it. So i try to draw it
(in this image, i just draw object O and A (without B), so i can understand what V_AO really mean)
(let say that A is traveling 0.5c from our viewpoint)

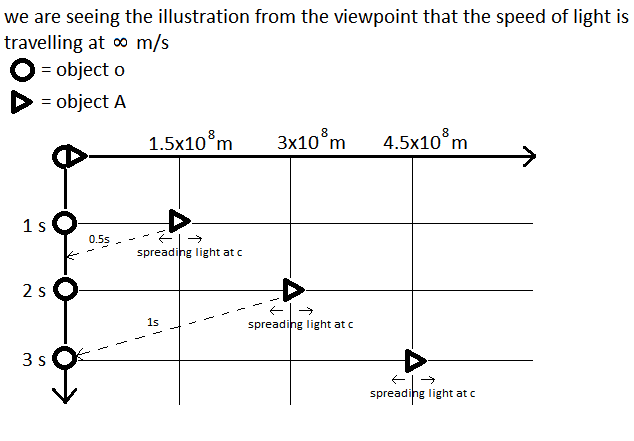
so, V_AO will be 1/3 c because O see A only travel 1.5x10⁸m after 1.5 second (or 3x10⁸m after 3 second), is this what we say A is moving relative to O?

 

[Vitro]

is this what we say A is moving relative to O?

No, A moving relative to O means that the position of A as measured by O (in O's coordinate system) changes over time. The relative speed $V_{OA}$ is the change in A's position $\Delta x$ over the interval of time $\Delta t$ (as measured in O's coordinates), and in your diagram it's just 0.5c. Nothing to do with what O sees (i.e. light from A reaching O).

 

[diazdaiz]

No, A moving relative to O means that the position of A as measured by O (in O's coordinate system) changes over time. The relative speed $V_{OA}$ is the change in A's position $\Delta x$ over the interval of time $\Delta t$ (as measured in O's coordinates), and in your diagram it's just 0.5c. Nothing to do with what O sees (i.e. light from A reaching O).

thank you very much, that's the keyword, its measured from O's coordinate

 

[Vitro]

thank you very much, that's the keyword, its measured from O's coordinate

The fact that A and O are moving relative to each other is invariant, you could use any inertial frame to make that determination. But if you want to measure their relative velocity then you need to use either A's or O's coordinates. Using a different frame of reference will give you what's called a closing or separation velocity which is not the same thing as their relative velocity.