SUMMARY
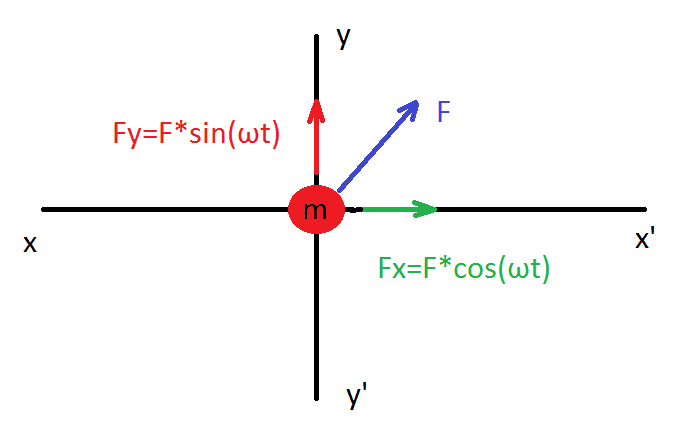
The discussion focuses on analyzing the motion of an object influenced by forces on the x and y axes, specifically using Newton's second law, represented as $$\vec F = m\vec a$$. Participants emphasize the importance of solving the differential equations for the velocity components $$v_x(t)$$ and $$v_y(t)$$ to determine the trajectory and distance traveled. The conversation also highlights the need for careful integration of velocity to obtain position, particularly addressing issues with negative distances and the correct application of integration bounds.
PREREQUISITES
- Understanding of Newton's second law of motion
- Familiarity with differential equations
- Knowledge of integration techniques in calculus
- Basic concepts of vector mathematics
NEXT STEPS
- Study the application of Newton's second law in two-dimensional motion
- Learn about solving differential equations for motion analysis
- Explore the integration of velocity functions to find position
- Investigate the implications of negative distances in physical motion
USEFUL FOR
Physics students, mechanical engineers, and anyone interested in the mathematical modeling of motion under forces.