Discussion Overview
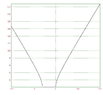
The discussion centers on the oblique asymptotes of the radical expression \(y = \sqrt{x^2 + 6x}\). Participants explore how to derive these asymptotes, particularly noting that this expression is not a rational function, which is typically associated with oblique asymptotes.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- Some participants note that oblique asymptotes are usually associated with rational expressions, yet \(y = \sqrt{x^2 + 6x}\) has asymptotes \(y = x + 3\) and \(y = -x - 3\).
- One participant suggests that for large \(x\), the asymptotic behavior can be approximated as \(\sqrt{x^2 + 6x} \sim x + 3\) for \(x \to +\infty\) and \(\sqrt{x^2 + 6x} \sim -(x + 3)\) for \(x \to -\infty\), but acknowledges the need for careful handling of the square root.
- Another participant proposes analyzing the difference \(f(x) - (ax + b)\) to derive the asymptote, providing a limit calculation to show that the function approaches the asymptote as \(x\) increases.
- A different approach is presented where the expression is squared and manipulated into a hyperbolic form, leading to the conclusion that the asymptotes are derived from the hyperbola's properties.
Areas of Agreement / Disagreement
Participants express varying methods to derive the asymptotes, and while they agree on the existence of the asymptotes, the methods and interpretations of the radical expression's behavior lead to different perspectives. No consensus is reached on a single method of derivation.
Contextual Notes
Some limitations include the dependence on the interpretation of asymptotic behavior and the handling of the square root function, which may introduce ambiguity in the analysis.
